题目内容
 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)椭圆E的内接平行四边形ABCD的一组对边分别过椭圆的焦点F1,F2,求该平行四边形面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件设椭圆E的方程为
+
=1,把点P(1,
)代入,能求出椭圆E的标准方程.
(Ⅱ)当直线AD的斜率不存在时,?ABCD的面积S=6.当直线AD的存在时,设其方程为y=k(x-1),设A(x1,y1),B(x2,y2),由
,得(3+4k2)x2-k2x+4k2-12=0,由此利用韦达定理求出?ABCD的面积S<6,由此求出符合条件的椭圆内接?ABCD的面积的最大值为6.
| x2 |
| 4c2 |
| y2 |
| 3c2 |
| 3 |
| 2 |
(Ⅱ)当直线AD的斜率不存在时,?ABCD的面积S=6.当直线AD的存在时,设其方程为y=k(x-1),设A(x1,y1),B(x2,y2),由
|
解答:
解:(Ⅰ)∵椭圆E:
+
=1(a>0,b>0)的离心率为
,且经过点P(1,
),
∴
=
,∴a2=4c2,b2=3c2,
∴椭圆E的方程为
+
=1,
把点P(1,
)代入,得
+
=1,解得c2=1,
∴椭圆E的标准方程为
+
=1.
(Ⅱ)当直线AD的斜率不存在时,直线AD的方程为x=1,
解方程组
,得A(1,
),D(1,-
),
∴?ABCD的面积S=6.
当直线AD的存在时,设其方程为y=k(x-1),设A(x1,y1),B(x2,y2),
由
,消去y整理,得:
(3+4k2)x2-k2x+4k2-12=0,
∴x1 +x2=
,x1x2=
,
∴|AD|=
•
=
,
又F1 (-1,0)到AD的距离d=
,
∴?ABCD的面积:
S=|AD|•d=
=6
=6
<6,
综上,符合条件的椭圆内接?ABCD的面积的最大值为6.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
∴椭圆E的方程为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
把点P(1,
| 3 |
| 2 |
| 1 |
| 4c2 |
| 3 |
| 4c2 |
∴椭圆E的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)当直线AD的斜率不存在时,直线AD的方程为x=1,
解方程组
|
| 3 |
| 2 |
| 3 |
| 2 |
∴?ABCD的面积S=6.
当直线AD的存在时,设其方程为y=k(x-1),设A(x1,y1),B(x2,y2),
由
|
(3+4k2)x2-k2x+4k2-12=0,
∴x1 +x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∴|AD|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 12(k2+1) |
| 3+4k2 |
又F1 (-1,0)到AD的距离d=
| 2|k| | ||
|
∴?ABCD的面积:
S=|AD|•d=
24|k|
| ||
| 3+4k2 |
|
1-
|
综上,符合条件的椭圆内接?ABCD的面积的最大值为6.
点评:本题考查椭圆方程的求法,考查平行四边形面积的最大值的求法,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
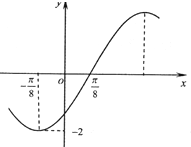 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<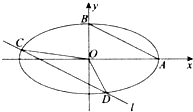 如图,A、B是椭圆
如图,A、B是椭圆