题目内容
如图是一个几何体的三视图，若它的体积为2，则a+b的最小值为考点：基本不等式在最值问题中的应用,简单空间图形的三视图
专题：计算题,空间位置关系与距离
分析：根据三视图判断几何体为三棱柱，且三棱柱的高为a，底面直角三角形的直角边长分别为b、1，利用三棱柱的体积公式求得ab=4，再利用基本不等式求a+b的最小值．
解答：
解：由三视图知几何体为三棱柱，且三棱柱的高为a，底面直角三角形的直角边长分别为b、1，
∴三棱柱的体积V=
×1×b×a=2，
∴ab=4，
∴a+b≥2
=4，当且仅当a=b=2时，取“=”．
故答案为：4．
∴三棱柱的体积V=
| 1 |
| 2 |
∴ab=4，
∴a+b≥2
| ab |
故答案为：4．
点评：本题考查了由三视图求几何体的体积，基本不等式的应用及棱柱的体积公式，判断几何体的形状及数据所对应的几何量是解答本题的关键．
练习册系列答案
相关题目
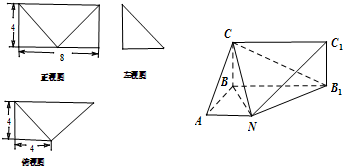已知某几何体的直观图和三视图如下图所示，其正视图为矩形，左视图为等腰直角三角形，俯视图为直角梯形．
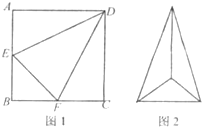如图1，边长为2的d正方形ABCD中，E，F 分别是AB，BC的中点，将△ADE，△CDF，△BEF折起，使A，C，B二点重合于G，所得二棱锥G-DEF的俯视图如图2，则其正视图的面积为如图是一个体积为10的空间几何体的三视图，则图中x的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
已知数列{an}是等比数列，且an＞0，若bn=log2an，则（ ）
| A、{bn}一定是递增的等差数列 |
| B、{bn}不可能是等比数列 |
| C、{2b2n-1+1}是等差数列 |
| D、{3bn}不是等比数列 |
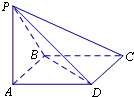如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PB⊥BC，PD⊥DC，且