题目内容
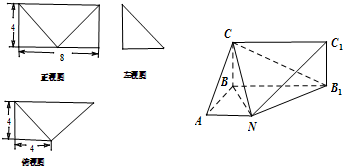 已知某几何体的直观图和三视图如下图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.(1)证明:BN⊥平面C1NB1;
(2)求二面角C-NB1-B的正切值的大小.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明BN⊥平面C1NB1,只需证明BN⊥B1C1,BN⊥B1N即可;
(2)证明∠CNB为所求二面角的平面角,在Rt△BCN中,可求二面角C-NB1-B的正切值的大小.
(2)证明∠CNB为所求二面角的平面角,在Rt△BCN中,可求二面角C-NB1-B的正切值的大小.
解答:
(1)证明:据题意易得B1C1⊥平面ABB1N,
∴BN⊥B1C1,
∵BN=4
,BB1=8,NB1=4
,
∴BN⊥B1N,
∵B1C1∩B1N=B1,
∴BN⊥平面C1NB1;
(2)解:∵BC⊥平面ABB1N,BN⊥B1N,
∴CN⊥B1N,
∴∠CNB为所求二面角的平面角.
在Rt△BCN中,tan∠CNB=
=
.
∴BN⊥B1C1,
∵BN=4
| 2 |
| 2 |
∴BN⊥B1N,
∵B1C1∩B1N=B1,
∴BN⊥平面C1NB1;
(2)解:∵BC⊥平面ABB1N,BN⊥B1N,
∴CN⊥B1N,
∴∠CNB为所求二面角的平面角.
在Rt△BCN中,tan∠CNB=
| 4 | ||
4
|
| ||
| 2 |
点评:本题考查线面垂直,考查面面角,解题的关键是正确运用线面垂直的判定定理,正确作出面面角.

练习册系列答案
相关题目
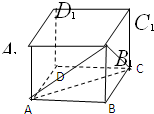 已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高.
已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高. 如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为
如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为