题目内容
已知正四棱锥P-ABCD,底面正方形的边长为1,侧棱长均为2,则二面角B-PC-D所成的平面角的余弦值为 .
考点:与二面角有关的立体几何综合题
专题:综合题,空间角
分析:作DE⊥PC,连接BE,则BE⊥PC,可得∠BED是二面角B-PC-D所成的平面角,求出三角形的三边,利用余弦定理,即可求出二面角B-PC-D所成的平面角的余弦值.
解答:
 解:作DE⊥PC,连接BE,则BE⊥PC,
解:作DE⊥PC,连接BE,则BE⊥PC,
∴∠BED是二面角B-PC-D所成的平面角,
△PCD中,PC=PD=2,CD=1,
∴由等面积可得
•1•
=
•2•DE,
∴DE=
,
∴BE=
,
∵BD=
,
∴由余弦定理可得cos∠BED=
=-
.
故答案为:-
.
 解:作DE⊥PC,连接BE,则BE⊥PC,
解:作DE⊥PC,连接BE,则BE⊥PC,∴∠BED是二面角B-PC-D所成的平面角,
△PCD中,PC=PD=2,CD=1,
∴由等面积可得
| 1 |
| 2 |
4-
|
| 1 |
| 2 |
∴DE=
| ||
| 4 |
∴BE=
| ||
| 4 |
∵BD=
| 2 |
∴由余弦定理可得cos∠BED=
| ||||||||
2•
|
| 1 |
| 15 |
故答案为:-
| 1 |
| 15 |
点评:本题考查面面角,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
下列说法中正确的是( )
| A、若p∨q为真命题,则p,q均为真命题 |
| B、命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0” |
| C、“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件 |
| D、在△ABC中,“a>b”是“sinA>sinB”的必要不充分条件 |
在△ABC中,tanB=-2,tanC=
,则A等于( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
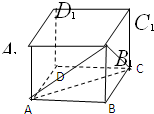 已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高.
已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高. 在△ABC中,∠BAC=120°,AB=
在△ABC中,∠BAC=120°,AB= 如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为
如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为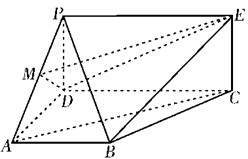 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=