Question

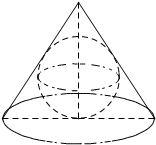一个轴截面是等边三角形的圆锥（即该圆锥的母线长与底面直径相等）有一个内切球，设内切球的体积为V₁，圆锥的体积为V₂，则V₁：V₂=

 

．

Answer 1

考点：旋转体（圆柱、圆锥、圆台）

专题：空间位置关系与距离

分析：作出轴截面，利用Rt△AOE∽Rt△ACD，求出球的半径OE（R）再计算球的体积和圆锥的体积，可得答案．

解答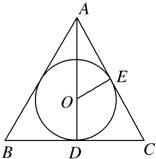： 解：如图所示，作出轴截面，
∵△ABC是正三角形，令AC=4，
则CD=

1

2

AC=2，
∴AD=

3

2

×4=2

3

；
∵Rt△AOE∽Rt△ACD，
∴OE：AO=CD：AC．
设OE=R，则AO=2

3

-R，
∴R：（2

3

-R）=1：2，
∴R=

2 3

3

．
∴内切球的体积为V₁=

4

3

πR³=

32 3

27

π，
圆锥的体积为V₂=

1

3

π•CD²•AD=

8 3

3

π，
∴V₁：V₂=

32 3

27

π：

8 3

3

π=4：9，
故答案为：4：9

点评：本题考查了空间几何体的体积的计算问题，解题的关键是求出球的半径，是基础题．