题目内容
已知函数f(x)=mx2-2(m+n)x+n,(m≠0)满足f(0)•f(1)>0,设x1,x2是方程f(x)=0的两根,则|x1-x2|的取值范围是 .
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:由f(0)•f(1)>0,即n(m+n)<0,再由二次方程的韦达定理,得到|x1-x2|=
=
=2
=2
,再由-1<
<0,即可得到范围.
| (x1+x2)2-4x1x2 |
=
|
1+
|
(
|
| n |
| m |
解答:
解:函数f(x)=mx2-2(m+n)x+n,(m≠0)满足f(0)•f(1)>0,
即有n(-m-n)>0,即n(m+n)<0,
由于x1,x2是方程f(x)=0的两根,
则4(m+n)2-4mn>0,x1+x2=
,x1x2=
,
则|x1-x2|=
=
=2
=2
,
由于n(m+n)<0,即有
<-1,则-1<
<0,
当
=-
,取得最小值2
=
,
→0时,|x1-x2|→2,
则有|x1-x2|∈[
,2).
故答案为:[
,2).
即有n(-m-n)>0,即n(m+n)<0,
由于x1,x2是方程f(x)=0的两根,
则4(m+n)2-4mn>0,x1+x2=
| 2(m+n) |
| m |
| n |
| m |
则|x1-x2|=
| (x1+x2)2-4x1x2 |
=
|
=2
1+
|
(
|
由于n(m+n)<0,即有
| m |
| n |
| n |
| m |
当
| n |
| m |
| 1 |
| 2 |
|
| 3 |
| n |
| m |
则有|x1-x2|∈[
| 3 |
故答案为:[
| 3 |
点评:本题考查二次函数的值域的求法,考查二次方程的韦达定理和运用,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}是各项均为正数的等比数列,公比q=3且a1a2a3…a30=330,则a3a6a9…a30=( )
| A、310 |
| B、315 |
| C、320 |
| D、325 |
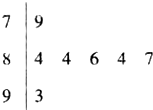 如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )
如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )| A、86,84 |
| B、84,84 |
| C、85,84 |
| D、85,93 |
(理科做) 定积分
(1-cosx)dx的值为( )
| ∫ | 2π 0 |
| A、2π | B、2π+1 |
| C、-2π | D、2π-1 |
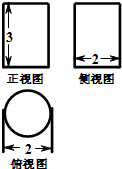 如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )
如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )| A、7π | B、8π |
| C、10π | D、π+12 |
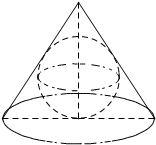 一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=
一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=