题目内容
已知f（x）+2f（
）=x（x≠0），求f（x）．
| 1 |
| x |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：首先，在所给的等式中，等号两边同时以
代x，得到一个等式f（
）+2f（x）=
，然后，联立方程组，把f（x）当做未知数，求解即可．
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答：
解：∵f（x）+2f（
）=x，①
等号两边同时以
代x，
得：f（
）+2f（x）=
，②
联立①②，
由①-2×②，解得
f（x）=-
+
，
∴函数f（x）的解析式：
f（x）=-
+
（x≠0）．
| 1 |
| x |
等号两边同时以
| 1 |
| x |
得：f（
| 1 |
| x |
| 1 |
| x |
联立①②，
由①-2×②，解得
f（x）=-
| x |
| 3 |
| 2 |
| 3x |
∴函数f（x）的解析式：
f（x）=-
| x |
| 3 |
| 2 |
| 3x |
点评：本题重点考查函数解析式的求解方法，构造法在解题中的应用，属于中档题．
练习册系列答案
相关题目
在数列{an}中，若a1=-2，且对任意的n∈N*有2an+1-2an=1，则数列{an}前15项的和为（ ）
A、
| ||
| B、30 | ||
| C、5 | ||
D、
|
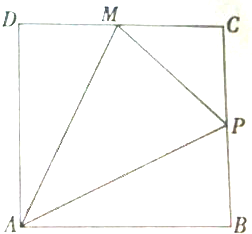如图，动点P在边长为1的正方形ABCD上运动，点M为CD的中点，当点P沿A→B→C→M运动时，点P经过的路程设为x，△APM的面积为f（x），求f（x）的解析式．