题目内容
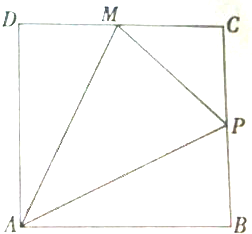 如图,动点P在边长为1的正方形ABCD上运动,点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM的面积为f(x),求f(x)的解析式.
如图,动点P在边长为1的正方形ABCD上运动,点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM的面积为f(x),求f(x)的解析式.考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:本题是一个分段函数,分点P在AB,BC和CM上得到三个一次函数,然后由一次函数的图象与性质确定选项.
解答:
解:当点P在AB上时,f(x)=x (0≤x≤1);
当点P在BC上时,PB=x-1,PC=2-x,
y=S正方形ABCD-S△ADM-S△ABP-S△PCM
=1-
-
(x-1)-
×
(2-x)=-
x+
,
∴f(x)=-
x+
(1<x≤2)
当点P在CM上时,MP=2.5-x,
∴f(x)=
(2.5-x)=-
x+
.(2<x≤2.5);
综上f(x)=
.
当点P在BC上时,PB=x-1,PC=2-x,
y=S正方形ABCD-S△ADM-S△ABP-S△PCM
=1-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∴f(x)=-
| 1 |
| 4 |
| 3 |
| 4 |
当点P在CM上时,MP=2.5-x,
∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
综上f(x)=
|
点评:本题考查的是动点问题的函数图象,分别考虑点O在AB,BC和CM上,由三角形的面积公式得到三个一次函数然后利用分段函数的形式表示.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知集合A={1,2a},B={a,b},若A∩B={
},则A∪B=( )
| 1 |
| 2 |
A、{-1,
| ||
B、{1,
| ||
C、{-1,
| ||
D、{1,
|
两直线3x+y-
m=0与6x+my+1=0平行,则它们之间的距离为( )
| 3 |
| 2 |
| A、4 | ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线C:2x2-y2=2,若过点P(1,2)直线l与C没有公共点,则l斜率的取值范围为( )
A、(-∞,-
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
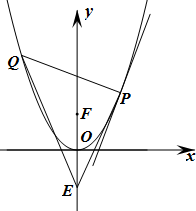 已知抛物线C的顶点在原点,焦点为F(0,1),准线与y轴的交点为E.
已知抛物线C的顶点在原点,焦点为F(0,1),准线与y轴的交点为E.