题目内容
已知函数y=
的定义域为[-3,6],求实数a,b的值.
| ax2+bx+18 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由已知,得到ax2+bx+18≥0的解集为[-3,6],所以方程ax2+bx+18=0的两根为-3,6,再由根与系数的关系得到a,b.
解答:
解:因为函数y=
的定义域为[-3,6],所以ax2+bx+18≥0的解集为[-3,6],
所以方程ax2+bx+18=0的两根为-3,6,
所以-3×6=
,-3+6=-
,所以a=-1,b=3.
| ax2+bx+18 |
所以方程ax2+bx+18=0的两根为-3,6,
所以-3×6=
| 18 |
| a |
| b |
| a |
点评:本题考查了函数的定义域以及一元二次方程与一元二次不等式的关系,经常考查,注意掌握.

练习册系列答案
相关题目
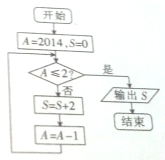 如图,该程序框图运行后输出的结果为( )
如图,该程序框图运行后输出的结果为( )| A、4024 | B、4026 |
| C、4028 | D、4020 |
两直线3x+y-
m=0与6x+my+1=0平行,则它们之间的距离为( )
| 3 |
| 2 |
| A、4 | ||||
B、
| ||||
C、
| ||||
D、
|
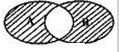 如图所示的韦恩图中,A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=
如图所示的韦恩图中,A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=