题目内容
二次函数y=f(x)的最小值等于4,且f(0)=f(2)=6
(1)求f(x)的解析式;
(2)若函数f(x)的定义域为[-1,4],求f(x)的值域;
(3)若函数f(x)的定义域为[a,a+1],f(x)的值域为[12,22],求a的值.
(1)求f(x)的解析式;
(2)若函数f(x)的定义域为[-1,4],求f(x)的值域;
(3)若函数f(x)的定义域为[a,a+1],f(x)的值域为[12,22],求a的值.
考点:函数解析式的求解及常用方法,函数的值域
专题:分类讨论,函数的性质及应用
分析:(1)根据题意,得出f(x)的对称轴,顶点坐标,从而求出解析式;
(2)由f(x)的解析式求出在[-1,4]上的最值,即得值域;
(3)讨论a的取值,得出f(x)在[a,a+1]上的单调性,从而求出f(x)在[a,a+1]上的值域,得出a的值.
(2)由f(x)的解析式求出在[-1,4]上的最值,即得值域;
(3)讨论a的取值,得出f(x)在[a,a+1]上的单调性,从而求出f(x)在[a,a+1]上的值域,得出a的值.
解答:
解:(1)根据题意,函数f(x)的对称轴是x=
=1,
∴顶点是(1,4);
∴设f(x)=a(x-1)2+4,
当x=0时,f(0)=a+4=6,
∴a=2;
∴f(x)=2(x-1)2+4=2x2-4x+6;
(2)∵f(x)的对称轴是x=1,
∴x=1时,f(x)min=f(1)=4;
x=4时,f(x)max=f(4)=22;
∴f(x)的值域是[4,22];
(3)①当a≥1时,f(x)在[a,a+1]上是增函数,
∴
,
即
,
解得a=3;
②当a≤0时,f(x)在[a,a+1]上是减函数,
∴
,
即
,
解得a=-2;
③当0<a<1时,f(x)在[a,a+1]上取得最小值
f(x)min=f(1)=4,不合题意;
综上,a=3或a=-2.
| 0+2 |
| 2 |
∴顶点是(1,4);
∴设f(x)=a(x-1)2+4,
当x=0时,f(0)=a+4=6,
∴a=2;
∴f(x)=2(x-1)2+4=2x2-4x+6;
(2)∵f(x)的对称轴是x=1,
∴x=1时,f(x)min=f(1)=4;
x=4时,f(x)max=f(4)=22;
∴f(x)的值域是[4,22];
(3)①当a≥1时,f(x)在[a,a+1]上是增函数,
∴
|
即
|
解得a=3;
②当a≤0时,f(x)在[a,a+1]上是减函数,
∴
|
即
|
解得a=-2;
③当0<a<1时,f(x)在[a,a+1]上取得最小值
f(x)min=f(1)=4,不合题意;
综上,a=3或a=-2.
点评:本题考查了求函数的解析式与值域的问题,解题时可以利用函数的图象与性质求出解析式,根据函数的单调性求出值域,是中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°
如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°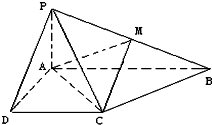 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=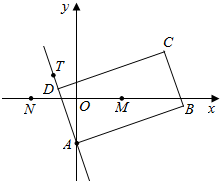 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为 如图,在半径为2
如图,在半径为2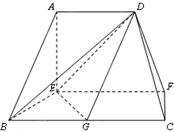 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.