题目内容
已知函数①f(x)=x2;②f(x)=lnx;③f(x)=ecosx;④f(x)=ex.其中对于f(x)定义域内的任意一个自变量x1都存在唯一的一个自变量x2,使f(x1)•f(x2)=1成立的函数是 (请填序号,多填、少填均不给分)
考点:抽象函数及其应用
专题:新定义,函数的性质及应用
分析:根据题中所给的新定义,试用选项中提供的函数,对新定义进行验证,选出符合新定义的函数序号.
解答:
解:①当f(x)=x2时,
对于f(x)定义域内的一个自变量x1=0,对于任意自变量x2,f(x1)=x12=0,f(x1)•f(x2)=0≠1.故函数①不符合题中条件;
②当f(x)=lnx时,
对于f(x)定义域内的一个自变量x1=1,对于任意自变量x2,f(x1)=lnx1=0,f(x1)•f(x2)=0≠1.故函数②不符合题中条件;
③当f(x)=ecosx时,
对于f(x)定义域内的任意一个自变量x1都存在一个自变量x2=π+x1,cosx2=cos(π+x1)=-cosx1,
f(x1)•f(x2)=ecosx1•ecosx2=ecosx1+cosx2=e0=1;
对于f(x)定义域内的任意一个自变量x1都存在一个自变量x2=3π+x1,cosx2=cos(3π+x1)=-cosx1,
f(x1)•f(x2)=ecosx1•ecosx2=ecosx1+cosx2=e0=1;
x2不惟一.故函数③不符合题中条件;
④当f(x)=ex时,
对于f(x)定义域内的任意一个自变量x1,存在唯一的一个自变量x2=-x1,f(x1)•f(x2)=ex1•ex2=ex1+x2=e0=1.
故函数④符合题中条件.
故答案为④.
对于f(x)定义域内的一个自变量x1=0,对于任意自变量x2,f(x1)=x12=0,f(x1)•f(x2)=0≠1.故函数①不符合题中条件;
②当f(x)=lnx时,
对于f(x)定义域内的一个自变量x1=1,对于任意自变量x2,f(x1)=lnx1=0,f(x1)•f(x2)=0≠1.故函数②不符合题中条件;
③当f(x)=ecosx时,
对于f(x)定义域内的任意一个自变量x1都存在一个自变量x2=π+x1,cosx2=cos(π+x1)=-cosx1,
f(x1)•f(x2)=ecosx1•ecosx2=ecosx1+cosx2=e0=1;
对于f(x)定义域内的任意一个自变量x1都存在一个自变量x2=3π+x1,cosx2=cos(3π+x1)=-cosx1,
f(x1)•f(x2)=ecosx1•ecosx2=ecosx1+cosx2=e0=1;
x2不惟一.故函数③不符合题中条件;
④当f(x)=ex时,
对于f(x)定义域内的任意一个自变量x1,存在唯一的一个自变量x2=-x1,f(x1)•f(x2)=ex1•ex2=ex1+x2=e0=1.
故函数④符合题中条件.
故答案为④.
点评:本题通过抽象函数的一个特征,研究了二次函数、对数函数、指数函数、三角函数的运算性质和规律.本题思维能力要求高,计算难度较大,属于中档题.

练习册系列答案
相关题目
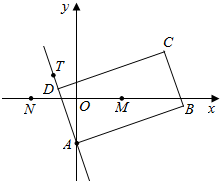 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为