题目内容
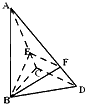 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且| AE |
| AC |
| AF |
| AD |
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)若λ=
| 1 |
| 2 |
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(I)要证不论λ为何值,总有EF⊥平面ABC,只需证CD⊥平面ABC,在△BCD中,根据∠BCD=90°得证.
(II)根据V三棱锥A-BEF=V三棱锥F-ABE,得出体积即可.
(II)根据V三棱锥A-BEF=V三棱锥F-ABE,得出体积即可.
解答:
 证明:(Ⅰ)∵AB⊥平面BCD,
证明:(Ⅰ)∵AB⊥平面BCD,
∴AB⊥CD,…(2分)
∵CD⊥BC,且AB∩BC=B,
∴CD⊥平面ABC,…(4分)
又∵
=
=λ(0<λ<1),
∴不论λ为何值,恒有EF∥CD,
∴EF⊥平面ABC,EF?平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC.…(6分)
(Ⅱ)∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=
,AB=
tan60°=
,
∴VA-BCD=
S△BCD•AB=
×
×
=
…(8分)
∵λ=
,∴E为AC的中点,又EF⊥平面ABC
VB-AFE=
S△ABE•EF=
S△ABC•EF=
×
×1×
×
=
…(10分)
∴VB-CDFE=VA-BCD-VB-AFE=
…(12分)
 证明:(Ⅰ)∵AB⊥平面BCD,
证明:(Ⅰ)∵AB⊥平面BCD,∴AB⊥CD,…(2分)
∵CD⊥BC,且AB∩BC=B,
∴CD⊥平面ABC,…(4分)
又∵
| AE |
| AC |
| AF |
| AD |
∴不论λ为何值,恒有EF∥CD,
∴EF⊥平面ABC,EF?平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC.…(6分)
(Ⅱ)∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=
| 2 |
| 2 |
| 6 |
∴VA-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
| ||
| 6 |
∵λ=
| 1 |
| 2 |
VB-AFE=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
| 6 |
| 1 |
| 2 |
| ||
| 24 |
∴VB-CDFE=VA-BCD-VB-AFE=
| ||
| 8 |
点评:本题考查考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.属于中档题.

练习册系列答案
相关题目
若m=(x+3)(x+7),n=(x+4)(x+6),则m,n的大小关系为( )
| A、m<n | B、m=n |
| C、m>n | D、不确定 |
 如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°
如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°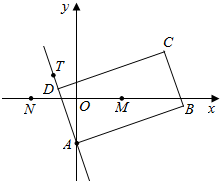 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为