题目内容
已知平面向量
=(-
,1),
=(
,
),
=-
+m
,
=cos2x
+sinx
,f(x)=
•
,x∈R.
(1)当m=2时,求y=f(x)的取值范围;
(2)设g(x)=f(x)-m2+2m+5,是否存在实数m,使得y=g(x)有最大值2,若存在,求出所有满足条件的m值,若不存在,说明理由.
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| c |
| 1 |
| 4 |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
(1)当m=2时,求y=f(x)的取值范围;
(2)设g(x)=f(x)-m2+2m+5,是否存在实数m,使得y=g(x)有最大值2,若存在,求出所有满足条件的m值,若不存在,说明理由.
考点:平面向量数量积的运算,两角和与差的正弦函数,正弦函数的定义域和值域
专题:平面向量及应用
分析:(1)当m=2时,求出
和
的坐标,可得函数y=f(x)=
•
=2-(sinx-1)2,再利用二次函数的性质求得函数的值域.
(2)根据
和
的坐标,求得函数y=f(x)=
•
=cos2x+msinx,可得g(x)的解析式.令sinx=t,则-1≤t≤1,g(x)=h(t)=-t2+mt-m2+2m+6,函数h(t)的对称轴为 t=
,再分当
<0时和当m≥0时两种情况,分别利用二次函数的单调性以及g(x)有最大值2,求得m的值,从而得出结论.
| c |
| d |
| c |
| d |
(2)根据
| c |
| d |
| c |
| d |
| m |
| 2 |
| m |
| 2 |
解答:
解:(1)当m=2时,
=-
+2
=(-
+1,
+
),
=cos2x
+sinx
=(
sinx-
cos2x,
sinx+cos2x ),
函数y=f(x)=
•
=(-
+1)•(
sinx-
cos2x )+(
+
)•(
sinx+cos2x )
=cos2x+2sinx=1-sin2x+2sinx=2-(sinx-1)2,
故当sinx=1时,函数y取得最大值为2,当sinx=-1时,函数y取得最小值为-2,
故函数的值域为[-2,2].
(2)∵
=-
+m
=(-
+
,
+
),
=cos2x
+sinx
=(
sinx-
cos2x,
sinx+cos2x ),
函数y=f(x)=
•
=(-
+
)•(
sinx-
cos2x )+(
+
)•(
sinx+cos2x )
=cos2x+msinx,
∴g(x)=f(x)-m2+2m+5=cos2x+msinx-m2+2m+5=1-sin2x+msinx-m2+2m+5
=-sin2x+msinx-m2+2m+6.
令sinx=t,则-1≤t≤1,g(x)=h(t)=-t2+mt-m2+2m+6,函数h(t)的对称轴为 t=
,
当
<0时,h(t)的最大值为h(1)=-1+m-m2+2m+6=2,求得m=
.
当m≥0时,h(t)的最大值为h(-1)=-1-m-m2+2m+6=2,求得m=
.
综上可得,存在实数m=
或m=
,使得y=g(x)有最大值2.
| c |
| 1 |
| 4 |
| a |
| b |
| ||
| 4 |
| 1 |
| 4 |
| 3 |
| d |
| a |
| b |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
函数y=f(x)=
| c |
| d |
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| ||
| 2 |
=cos2x+2sinx=1-sin2x+2sinx=2-(sinx-1)2,
故当sinx=1时,函数y取得最大值为2,当sinx=-1时,函数y取得最小值为-2,
故函数的值域为[-2,2].
(2)∵
| c |
| 1 |
| 4 |
| a |
| b |
| ||
| 4 |
| m |
| 2 |
| 1 |
| 4 |
m
| ||
| 2 |
| d |
| a |
| b |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
函数y=f(x)=
| c |
| d |
| ||
| 4 |
| m |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 4 |
m
| ||
| 2 |
| ||
| 2 |
=cos2x+msinx,
∴g(x)=f(x)-m2+2m+5=cos2x+msinx-m2+2m+5=1-sin2x+msinx-m2+2m+5
=-sin2x+msinx-m2+2m+6.
令sinx=t,则-1≤t≤1,g(x)=h(t)=-t2+mt-m2+2m+6,函数h(t)的对称轴为 t=
| m |
| 2 |
当
| m |
| 2 |
3-
| ||
| 2 |
当m≥0时,h(t)的最大值为h(-1)=-1-m-m2+2m+6=2,求得m=
1+
| ||
| 2 |
综上可得,存在实数m=
3-
| ||
| 2 |
1+
| ||
| 2 |
点评:本题主要考查两个向量的数量积的运算,二次函数的性质,求函数的最值,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
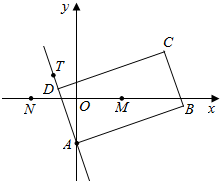 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为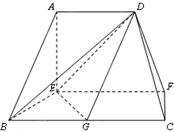 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.