题目内容
若cos(α+
)-sinα=
,则cos(α+
)= .
| π |
| 6 |
3
| ||
| 5 |
| π |
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:通过两角和公式对已知等式整理后求得
cosα-
sinα的值,进而利用两角和公式求得答案.
| ||
| 2 |
| 3 |
| 2 |
解答:
解:∵cos(α+
)-sinα=
,
cosα-
sinα=
,
∴
(
cosα-
sinα)=
cos(α+
)=
,
∴cos(α+
)=
.
故答案为:
.
| π |
| 6 |
3
| ||
| 5 |
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 5 |
∴
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
3
| ||
| 5 |
∴cos(α+
| π |
| 3 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题主要考查了两角和与差的正弦函数.要求对两角和与差的正弦函数与余弦函数公式灵活运用.

练习册系列答案
相关题目
“函数y=ax单调递减”是“lna<1”的什么条件.( )
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
若tanα=3,则
的值等于( )
| 4sinα-2cosα |
| 5cosα+3sinα |
A、
| ||
B、
| ||
| C、1 | ||
D、-
|
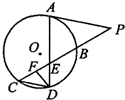 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,AE=12,ED=6,EF=4,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,AE=12,ED=6,EF=4,则PB=
