题目内容
函数y=ln（x+2）在点（-1，0）处的切线方程为（ ）
| A、x+y+1=0 |
| B、x-y+1=0 |
| C、x-2y+1=0 |
| D、x+2y+1=0 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到函数y=ln（x+2）在x=-1处的导数，由直线方程的点斜式得切线方程．
解答：
解：由y=ln（x+2），得y′=
，
∴y′|x=-1=1，
即函数y=ln（x+2）在点（-1，0）处的切线的斜率为1，
∴函数y=ln（x+2）在点（-1，0）处的切线方程为y=1×（x+1），
即x-y+1=0．
故选：B．
| 1 |
| x+2 |
∴y′|x=-1=1，
即函数y=ln（x+2）在点（-1，0）处的切线的斜率为1，
∴函数y=ln（x+2）在点（-1，0）处的切线方程为y=1×（x+1），
即x-y+1=0．
故选：B．
点评：本题考查利用导数研究曲线上某点处的切线方程，曲线过某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
某四棱锥的三视图如图所示，则该四棱锥的体积是（ ）
| A、27 | ||
| B、9 | ||
C、3
| ||
| D、3 |
若某程序框图如图所示，则输出的n的值是（ ）
| A、3 | B、4 | C、5 | D、6 |
一个四面体的四个顶点在空间直角坐标系O-xyz中的坐标分别是（0，0，0），（1，2，0），（0，2，2），（3，0，1），则该四面体中以yOz平面为投影面的正视图的面积为（ ）
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
设全集U=R，A={x|x2-2x≤0}，B={y|y=cosx，x∈R}，则图中阴影部分表示的区间是（ ）
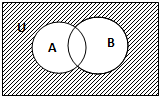
| A、[0，1] |
| B、[-1，2] |
| C、（-∞，-1）∪（2，+∞） |
| D、（-∞，-1]∪[2，+∞） |
执行如图所示的程序框图，如果输入a=2，那么输出的结果为（ ）
| A、2 | B、3 | C、4 | D、5 |
已知圆E的圆心在x轴上，且与y轴切于原点．过抛物线y2=2px（p＞0）焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点．已知l截圆所得的弦长为
如图，设点P在曲线y=x2，从原点向A（2，4）移动，让直线OP与曲线y=x2所围成图形面积为S1，直线OP、直线x=2与曲线y=x2所围成图形的面积为S2．