题目内容
对于自然数数组(a,b,c),如下定义该数组的极差:三个数的最大值与最小值的差.如果(a,b,c)的极差d≥1,可实施如下操作f:若a,b,c中最大的数唯一,则把最大数减2,其余两个数各增加1;若a,b,c中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为f1(a,b,c),其级差为d1.若d1≥1,则继续对f1(a,b,c)实施操作f,…,实施n次操作后的结果记为fn(a,b,c),其极差记为dn.例如:f1(1,3,3)=(3,2,2),f2(1,3,3)=(1,3,3).
(Ⅰ)若(a,b,c)=(1,3,14),求d1,d2和d2014的值;
(Ⅱ)已知(a,b,c)的极差为d且a<b<c,若n=1,2,3,…时,恒有dn=d,求d的所有可能取值;
(Ⅲ)若a,b,c是以4为公比的正整数等比数列中的任意三项,求证:存在n满足dn=0.
(Ⅰ)若(a,b,c)=(1,3,14),求d1,d2和d2014的值;
(Ⅱ)已知(a,b,c)的极差为d且a<b<c,若n=1,2,3,…时,恒有dn=d,求d的所有可能取值;
(Ⅲ)若a,b,c是以4为公比的正整数等比数列中的任意三项,求证:存在n满足dn=0.
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(Ⅰ)根据极差的定义,结合(a,b,c)=(1,3,14),可求d1,d2和d2014的值;
(Ⅱ)分类讨论,由操作规则,尽快求出dn=d时,d的所有可能取值;
(Ⅲ)先证明(a,b,c)的极差d0是3的倍数,依据操作f的规则,当在三元数组fi(a,b,c)(i=1,2,3,…x,x∈N)中,总满足ci是唯一最大数,ai是最小数时,一定有a+x<b+x<c-2x,解得x<
;依据操作f的规则,当在三元数组fi(a,b,c)(i=
,
+1,…
+y,y∈N)中,总满足ci=bi是最大数,ai是最小数时,一定有
+2y<
-y,解得y<
,即可得出结论.
(Ⅱ)分类讨论,由操作规则,尽快求出dn=d时,d的所有可能取值;
(Ⅲ)先证明(a,b,c)的极差d0是3的倍数,依据操作f的规则,当在三元数组fi(a,b,c)(i=1,2,3,…x,x∈N)中,总满足ci是唯一最大数,ai是最小数时,一定有a+x<b+x<c-2x,解得x<
| c-b |
| 3 |
| c-b |
| 3 |
| c-b |
| 3 |
| c-b |
| 3 |
| 3a+c-b |
| 3 |
| c+2b |
| 3 |
| b-a |
| 3 |
解答:
(Ⅰ)解:由题意,d1=10,d2=7,d2014=2---------------------------(3分)
(Ⅱ)解:①当d=2时,则(a,b,c)=(a,a+1,a+2)
所以f1(a,a+1,a+2)=(a+1,a+2,a),d1=a+2-a=2,
由操作规则可知,每次操作,数组中的最大数a+2变为最小数a,最小数a和次小数a+1分别变为次小数a+1和最大数a+2,所以数组的极差不会改变.
所以,当d=2时,dn=d(n=1,2,3,…)恒成立.
②当d≥3时,则f1(a,b,c)=(a+1,b+1,c-2)
所以d1=b+1-(a+1)=b-a<c-a=d或d1=c-2-(a+1)=d-3
所以总有d1≠d.
综上讨论,满足dn=d(n=1,2,3,…)的d的取值仅能是2.---------------------(8分)
(Ⅲ)证明:因为a,b,c是以4为公比的正整数等比数列的三项,
所以a,b,c是形如m•4k(其中m∈N*)的数,
又因为4k=(3+1)k=3k+
•3k-1+…+1
所以a,b,c中每两个数的差都是3的倍数.
所以(a,b,c)的极差d0是3的倍数.------------------------------------------------(9分)
设fi(a,b,c)=(ai,bi,ci),不妨设a<b<c,
依据操作f的规则,当在三元数组fi(a,b,c)(i=1,2,3,…x,x∈N)中,总满足ci是唯一最大数,ai是最小数时,一定有a+x<b+x<c-2x,解得x<
.
所以,当i=1,2,3,…
-1时,di=ci-ai=(ci-1-2)-(ai-1+1)=di-1-3.
f
(a,b,c)=(
,
,
),d
=b-a
依据操作f的规则,当在三元数组fi(a,b,c)(i=
,
+1,…
+y,y∈N)中,总满足ci=bi是最大数,ai是最小数时,一定有
+2y<
-y,解得y<
.
所以,当i=
,
+1,…,
-1时,di=ci-ai=(ci-1-1)-(ai-1+2)=di-1-3.
f
(a,b,c)=(
,
,
),d
=0
所以存在n=
,满足fn(a,b,c)的极差dn=0.----------------------------(13分)
(Ⅱ)解:①当d=2时,则(a,b,c)=(a,a+1,a+2)
所以f1(a,a+1,a+2)=(a+1,a+2,a),d1=a+2-a=2,
由操作规则可知,每次操作,数组中的最大数a+2变为最小数a,最小数a和次小数a+1分别变为次小数a+1和最大数a+2,所以数组的极差不会改变.
所以,当d=2时,dn=d(n=1,2,3,…)恒成立.
②当d≥3时,则f1(a,b,c)=(a+1,b+1,c-2)
所以d1=b+1-(a+1)=b-a<c-a=d或d1=c-2-(a+1)=d-3
所以总有d1≠d.
综上讨论,满足dn=d(n=1,2,3,…)的d的取值仅能是2.---------------------(8分)
(Ⅲ)证明:因为a,b,c是以4为公比的正整数等比数列的三项,
所以a,b,c是形如m•4k(其中m∈N*)的数,
又因为4k=(3+1)k=3k+
| C | 1 k |
所以a,b,c中每两个数的差都是3的倍数.
所以(a,b,c)的极差d0是3的倍数.------------------------------------------------(9分)
设fi(a,b,c)=(ai,bi,ci),不妨设a<b<c,
依据操作f的规则,当在三元数组fi(a,b,c)(i=1,2,3,…x,x∈N)中,总满足ci是唯一最大数,ai是最小数时,一定有a+x<b+x<c-2x,解得x<
| c-b |
| 3 |
所以,当i=1,2,3,…
| c-b |
| 3 |
f
| c-b |
| 3 |
| 3a+c-b |
| 3 |
| c+2b |
| 3 |
| c+2b |
| 3 |
| c-b |
| 3 |
依据操作f的规则,当在三元数组fi(a,b,c)(i=
| c-b |
| 3 |
| c-b |
| 3 |
| c-b |
| 3 |
| 3a+c-b |
| 3 |
| c+2b |
| 3 |
| b-a |
| 3 |
所以,当i=
| c-b |
| 3 |
| c-b |
| 3 |
| c-a |
| 3 |
f
| c-a |
| 3 |
| a+b+c |
| 3 |
| a+b+c |
| 3 |
| a+b+c |
| 3 |
| c-a |
| 3 |
所以存在n=
| c-a |
| 3 |
点评:本题考查数列的应用,考查新定义,考查学生分析解决问题的能力,考查分类讨论的数学思想,难度大.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知p=
,q=
-
,r=
-
,则p,q,r的大小为( )
| 2 |
| 7 |
| 3 |
| 6 |
| 2 |
| A、p>q>r |
| B、p>r>q |
| C、q>p>r |
| D、q>r>p |
设全集U=R,A={x|x2-2x≤0},B={y|y=cosx,x∈R},则图中阴影部分表示的区间是( )
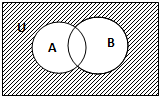

| A、[0,1] |
| B、[-1,2] |
| C、(-∞,-1)∪(2,+∞) |
| D、(-∞,-1]∪[2,+∞) |
 已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为
已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为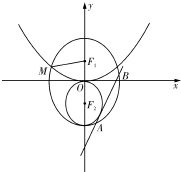 已知F1,F2是椭圆C1:
已知F1,F2是椭圆C1: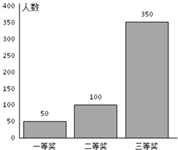 某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.