题目内容
已知i为虚数单位，a，b∈R，i（a+i）=b+2i，则a+b等于（ ）
| A、-1 | B、1 | C、-3 | D、3 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由条件利用两个复数代数形式的乘法，两个复数相等的条件，求出a和b的值，可得a+b．
解答：
解：∵i（a+i）=b+2i，即-1+ai=b+2i，∴b=-1，且a=2，
∴a+b=1，
故选：B．
∴a+b=1，
故选：B．
点评：本题主要考查两个复数相等的条件，两个复数代数形式的乘法，属于基础题．
练习册系列答案
相关题目
已知全集为R，集合A={x|x≥1}，那么集合∁RA等于（ ）
| A、{x|x＞1} |
| B、{x|x＞-1} |
| C、{x|x＜1} |
| D、{x|x＜-1} |
对两个变量x与y进行回归分析，得到一组样本数据：（1，1），（2，1.5），（4，3），（5.4.5），若甲同学根据这组数据得到的回归模型1：
=x-1，乙同学根据这组数据得到的回归模型2：
=
x+
，则（ ）
 |
| y |
|
| y |
| 1 |
| 2 |
| 1 |
| 2 |
| A、型1的拟合精度高 |
| B、模型2的拟合精度高 |
| C、模型1和模型2的拟合精度一样 |
| D、无法判断哪个模型的拟合精度高 |
设全集U=R，A={x|x2-2x≤0}，B={y|y=cosx，x∈R}，则图中阴影部分表示的区间是（ ）
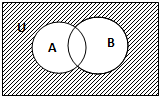
| A、[0，1] |
| B、[-1，2] |
| C、（-∞，-1）∪（2，+∞） |
| D、（-∞，-1]∪[2，+∞） |
一个棱锥被平行于底面的平面所截，若截面面积与底面面积之比为4：9，则此棱锥的侧棱被分成的上、下两部分长度之比为（ ）
| A、4：9 | ||
| B、2：1 | ||
| C、2：3 | ||
D、2：
|
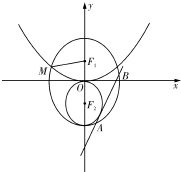已知F1，F2是椭圆C1：