题目内容
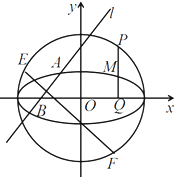 如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.
如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.(1)求点M的轨迹Γ的方程;
(2)设动直线l与⊙O相交所得的弦长为定值2
| 3 |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)利用中点坐标公式,确定P,M坐标之间的关系,将P的坐标代入圆的方程,即可求得M的轨迹方程;
(2)设l:y=kx+m(k≠0),利用动直线l与⊙O相交所得的弦长为定值2
,圆的半径为2,可得
=1;直线代入椭圆方程,求出AB的中垂线方程,利用O到直线EF的距离为d=
,d最大时,|EF|最小,即可得出结论.
(2)设l:y=kx+m(k≠0),利用动直线l与⊙O相交所得的弦长为定值2
| 3 |
| |m| | ||
|
|
| ||
|
解答:
解:(1)设M(x,y),则P(x,2y)
∵P在圆x2+y2=4上,
∴x2+4y2=4,
∴点M的轨迹Γ的方程是x2+4y2=4;
(2)设l:y=kx+m(k≠0),则
∵动直线l与⊙O相交所得的弦长为定值2
,圆的半径为2,
∴O到直线l的距离为1,即
=1,
直线代入椭圆方程,可得(1+4k2)x2+8kmx+(4m2-4)=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
,
∴AB的中点为(-
,
),AB的中垂线方程为y-
=-
(x+
),
化简可得x+ky+
=0,
O到直线EF的距离为d=
,d最大时,|EF|最小.
将
=1代入d=
,可得d=
,
∵1+4k2≥4|k|,∴d≤
(当且仅当|k|=
时取等号),
∴|EF|≥2
=
,即|EF|的最小值为
.
∵P在圆x2+y2=4上,
∴x2+4y2=4,
∴点M的轨迹Γ的方程是x2+4y2=4;
(2)设l:y=kx+m(k≠0),则
∵动直线l与⊙O相交所得的弦长为定值2
| 3 |
∴O到直线l的距离为1,即
| |m| | ||
|
直线代入椭圆方程,可得(1+4k2)x2+8kmx+(4m2-4)=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
| 8km |
| 1+4k2 |
∴AB的中点为(-
| 4km |
| 1+4k2 |
| m |
| 1+4k2 |
| m |
| 1+4k2 |
| 1 |
| k |
| 4km |
| 1+4k2 |
化简可得x+ky+
| 3km |
| 1+4k2 |
O到直线EF的距离为d=
|
| ||
|
将
| |m| | ||
|
|
| ||
|
| |3k| |
| 1+4k2 |
∵1+4k2≥4|k|,∴d≤
| 3 |
| 4 |
| 1 |
| 2 |
∴|EF|≥2
22-(
|
| ||
| 2 |
| ||
| 2 |
点评:本题考查轨迹方程,考查代入法的运用,考查直线与椭圆的位置关系,考查学生的计算能力,确定坐标之间的关系是关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
若某程序框图如图所示,则输出的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
 已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为
已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为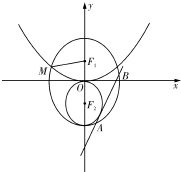 已知F1,F2是椭圆C1:
已知F1,F2是椭圆C1: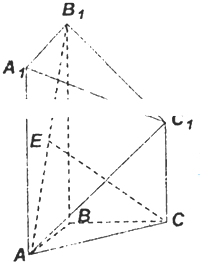 如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点.
如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点. 如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.
如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.