题目内容
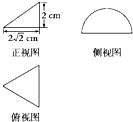 一个几何体的三视图及其尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为( )
一个几何体的三视图及其尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为( )A、2(1+2
| ||||
B、2(1+
| ||||
C、4(1+
| ||||
D、2(2+
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是半圆锥,根据三视图的数据判断底面半径与高,求母线长,把数据代入表面积公式计算.
解答:
解:由三视图知:几何体是半圆锥,
其中底面半径为2,高为2
.∴母线长为
=2
.
∴几何体的表面积S=
π×22+
×4×2
+
×π×2×2
=2π+4
+2
π.
故选:B.
其中底面半径为2,高为2
| 2 |
| 4+8 |
| 3 |
∴几何体的表面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
故选:B.
点评:本题考查了由三视图求几何体的表面积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.

练习册系列答案
相关题目
由函数y=cosx与x=0,x=
π,y=0围成的几何图形的面积为( )
| 5 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i为虚数单位,a为实数,复数z=(a-2i)•i在复平面内对应的点为M,则“a=-1”是“点M在第四象限”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=(-1,1),
=(3,m),若
⊥
,则实数m=( )
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、3 | D、-3 |
在△ABC中,∠C=90°,P为三角形内一点且S△PAB=S△PBC=S△PCA,则
=( )
| PA2+PB2 |
| PC2 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、5 |
已知f(x)=sinωx+
cosωx(ω>0)的两条相邻的对称轴间的距离为
,且f(x)图象关于点(x0,0)成中心对称,则x0可能为( )
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知角θ的顶点与原点重合,始边与x轴的非负半轴重合,终边在直线y=2x上,则sin2θ等于( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
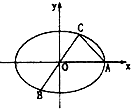 如图,已知椭圆
如图,已知椭圆