题目内容
已知向量
=（-1，1），
=（3，m），若
⊥
，则实数m=（ ）
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、3 | D、-3 |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：利用向量垂直的充要条件数量积为0；利用向量的数量积公式列出方程求出m的值．
解答：
解：向量
=（-1，1），
=（3，m），若
⊥
，
则
•
=0，
即-3+m=0，
∴m=3．
故选：C．
| a |
| b |
| a |
| b |
则
| a |
| b |
即-3+m=0，
∴m=3．
故选：C．
点评：本题考查向量的数量积运算与向量垂直的充要条件，属容易题．
练习册系列答案
相关题目
在数列{an}中，有an+an+1+an+2（n∈N*）为定值，且a100=2，a200=3，a300=4，则此数列{an}的前2014项的和S2014=（ ）
| A、6039 | B、6042 |
| C、6043 | D、6041 |
| a |
| b |
| a |
| b |
| a |
| b |
| A、锐角 | B、直角 | C、钝角 | D、π |
已知向量
与向量
的夹角为90°，且|
|=1，|
|=2，若
=
+λ
，
⊥（2
-
），则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
A、λ=
| ||
B、λ=
| ||
C、λ=
| ||
| D、λ=1 |
某校对高三年级1200名学生进行健康检查，按性别用分层抽样的方法抽取一个容量为120人的样本．已知女生抽到了55人，则该校男生的人数是（ ）
| A、65 | B、550 |
| C、600 | D、650 |
若存在正实数M，对于任意x∈（1，+∞），都有|f（x）|≤M，则称函数f（x）在（1，+∞） 上是有界函数．下列函数：
①f（x）=
；
②f（x）=
；
③f（x）=
；
④f（x）=xsinx．
其中“在（1，+∞）上是有界函数”的序号为（ ）
①f（x）=
| 1 |
| x-1 |
②f（x）=
| x |
| x2+1 |
③f（x）=
| lnx |
| x |
④f（x）=xsinx．
其中“在（1，+∞）上是有界函数”的序号为（ ）
| A、②③ | B、①②③ |
| C、②③④ | D、③④ |
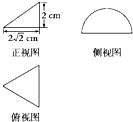一个几何体的三视图及其尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，则这个几何体的表面积为（ ）A、2（1+2
| ||||
B、2（1+
| ||||
C、4（1+
| ||||
D、2（2+
|