题目内容
在△ABC中,∠C=90°,P为三角形内一点且S△PAB=S△PBC=S△PCA,则
=( )
| PA2+PB2 |
| PC2 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、5 |
考点:三角形的面积公式
专题:综合题,解三角形
分析:确定P是Rt△ABC的重心,利用三角形中线公式,可得PA2+PB2=5PC2,从而可得结论.
解答:
解:已知△ABC是直角三角形,AB为斜边,记AB=c,BC=a,CA=b,则有c2=a2+b2.
∵S△PAB=S△PBC=S△PCA,
∴P是Rt△ABC的重心.
设mc,ma,mb分别表示Rt△ABC的对应边AB,BC,CA上的中线,则有
PC=
,PA=
,PB=
.
而三角形中线公式为4(mc)2=2a2+2b2-c2=c2,
4(ma)2=2b2+2c2-a2,4(mb)2=2c2+2a2-b2.
∴4(ma)2+4(mb)2=5c2,
∴4(ma)2+4(mb)2=20(mc)2,
∴PA2+PB2=5PC2,
∴
=5,
故选:D.
∵S△PAB=S△PBC=S△PCA,
∴P是Rt△ABC的重心.
设mc,ma,mb分别表示Rt△ABC的对应边AB,BC,CA上的中线,则有
PC=
| 2mc |
| 3 |
| 2ma |
| 3 |
| 2mb |
| 3 |
而三角形中线公式为4(mc)2=2a2+2b2-c2=c2,
4(ma)2=2b2+2c2-a2,4(mb)2=2c2+2a2-b2.
∴4(ma)2+4(mb)2=5c2,
∴4(ma)2+4(mb)2=20(mc)2,
∴PA2+PB2=5PC2,
∴
| PA2+PB2 |
| PC2 |
故选:D.
点评:本题考查三角形面积的计算,考查三角形中线公式,考查学生的计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
已知x∈R,则“x<0”是“x<cosx”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列四个图中,函数y=
的图象可能是( )
| 10ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |
某校对高三年级1200名学生进行健康检查,按性别用分层抽样的方法抽取一个容量为120人的样本.已知女生抽到了55人,则该校男生的人数是( )
| A、65 | B、550 |
| C、600 | D、650 |
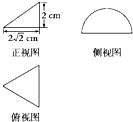 一个几何体的三视图及其尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为( )
一个几何体的三视图及其尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为( )A、2(1+2
| ||||
B、2(1+
| ||||
C、4(1+
| ||||
D、2(2+
|
已知x与y之间的一组数据如表所示,则x与y的回归直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A、(2,2) |
| B、(1.5,0) |
| C、(1,2) |
| D、(1.5,4) |
执行如图所示的程序框图,则输出的n为( )


| A、4 | B、5 | C、6 | D、7 |
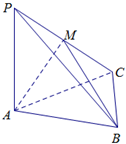 如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题:
如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题: