题目内容
由函数y=cosx与x=0,x=
π,y=0围成的几何图形的面积为( )
| 5 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:定积分在求面积中的应用
专题:导数的概念及应用
分析:作出函数对应的图象,根据积分的几何意义求几何图形的面积.
解答:
 解:函数的图象如图:
解:函数的图象如图:
根据积分的几何意义可知,所求区域面积为S=
|cosx|dx=
cosxdx-
cosxdx
=sinx
-sinx
=1-(
-1)=
.
故选:D.
 解:函数的图象如图:
解:函数的图象如图:根据积分的几何意义可知,所求区域面积为S=
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
|
=sinx
| | |
0 |
| | |
|
| 1 |
| 2 |
| 3 |
| 2 |
故选:D.
点评:本题主要考查定积分的应用,在利用定积分求面积时必须要求被积函数f(x)≥0,要求熟练掌握常见函数的积分公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数
(i为虚数单位)的模等于( )
| 1+i |
| i |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
在数列{an}中,有an+an+1+an+2(n∈N*)为定值,且a100=2,a200=3,a300=4,则此数列{an}的前2014项的和S2014=( )
| A、6039 | B、6042 |
| C、6043 | D、6041 |
已知x∈R,则“x<0”是“x<cosx”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
Rt△ABC中CA=CB=
,M为AB的中点,将△ABC沿CM折叠,使A、B之间的距离为1,则三棱锥M-ABC外接球的表面积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、3π | ||
D、
|
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| a |
| b |
| a |
| b |
| a |
| b |
| A、锐角 | B、直角 | C、钝角 | D、π |
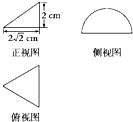 一个几何体的三视图及其尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为( )
一个几何体的三视图及其尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为( )A、2(1+2
| ||||
B、2(1+
| ||||
C、4(1+
| ||||
D、2(2+
|