题目内容
等差数列{an}的前 n项和为{Sn}，若S8-S4=36，a6=2a4，则a1=（ ）
| A、-2 | B、0 | C、2 | D、4 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：等差数列{an}的前n项和为{Sn}，由已知得
，由此能求出结果．
|
解答：
解：∵等差数列{an}的前n项和为{Sn}，
S8-S4=36，a6=2a4，
∴
，
解得a1=-2，d=2．
故选：A．
S8-S4=36，a6=2a4，
∴
|
解得a1=-2，d=2．
故选：A．
点评：本题考查等差数列的首项的求法，是基础题，解题时要认真审题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
f（x）是R上周期为3的奇函数，若f（1）＜1，f（2）=a2+a-1，则a的取值范围是（ ）
| A、a＜0.5且a≠1 |
| B、-1＜a＜0 |
| C、a＜-1或a＞0 |
| D、-1＜a＜2 |
若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中的真命题是（ ）
| A、若m?β，α⊥β，则m⊥α |
| B、若α∩γ=m，β∩γ=n，m∥n，则α∥β |
| C、若m⊥β，m∥α，则α⊥β |
| D、若α⊥γ，α⊥β，则β⊥γ |
已知函数f（x）的图象如图所示，则f（x）的解析式可以为（ ）
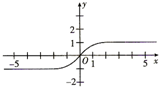
A、f（x）=x
| |||||||||
B、f（x）=
| |||||||||
C、f（x）=
| |||||||||
D、f（x）=
|
对于每一个实数x，f（x）是y=-x2+4和y=3x这两个函数中较小者，则f（x）的最大值是（ ）
| A、3 | B、4 | C、0 | D、-4 |
已知△ABC中，a=1，b=2，c=
，则∠C的大小为（ ）
| 7 |
| A、30° |
| B、120° |
| C、60°或80° |
| D、30°或150° |
已知向量
=（-1，2），
=（5，k），若
∥
，则实数k的值为（ ）
| a |
| b |
| a |
| b |
| A、5 | B、-5 | C、10 | D、-10 |