题目内容
凼数y=
的值域是 .
| x-3 |
| x+1 |
考点:函数的值域
专题:函数的性质及应用
分析:本题宜用分离常数法求值域,将函数可以变为y=1-
,再由函数的单调性求值域.
| 4 |
| x+1 |
解答:
解:由题函数的定义域为{x|x≠-1}
函数y=
=
=1-
≠1,
故函数的值域为{y|y≠1}
故答案为:{y|y≠1}
函数y=
| x-3 |
| x+1 |
| x+1-4 |
| x+1 |
| 4 |
| x+1 |
故函数的值域为{y|y≠1}
故答案为:{y|y≠1}
点评:本题考点是函数的值域,本题求值域采用了分离常数法的技巧,对于分式形函数单调性的判断是一个好办法,注意总结这种技巧的适用范围以及使用规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( )| A、π | B、2π | C、3π | D、4π |
设F1,F2是双曲线
-
=1(a>0,b>0)的左右两个焦点,若在双曲线的右支上存在一点P,使(
+
)•
=0(O为原点)且|PF1|=
|PF2|,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| OF2 |
| F2P |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若点A是棱长为2的正方体的一个顶点,在这个正方体内随机取一个点P,则点P到点A的距离大于2的概率为( )
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、
|
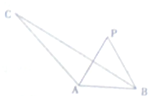 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.