题目内容
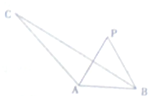 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.(1)求BC的长;
(2)若α=30°时,求S的值.
考点:正弦定理
专题:解三角形
分析:(1)由题意和余弦定理求出边BC的长;
(2)由P为∠BAC平分线上异于A的一点求出∠APB,再由内角和定理求出∠ABP,即可求出角形PAB的面积S.
(2)由P为∠BAC平分线上异于A的一点求出∠APB,再由内角和定理求出∠ABP,即可求出角形PAB的面积S.
解答:
解:(1)由题意得,在△ABC中,∠BAC=120°,AC=3,AB=1,
由余弦定理得,BC2=AB2+AC2-2AB•ACcos∠BAC
=1+9-2×1×3×(-
)=13,
所以BC=
;
(2)因为P为∠BAC平分线上异于A的一点,所以∠PAB=60°,
又∠APB=30°,则∠ABP=180°-60°-30°=90°,
又AB=1,则PB=
,
所以三角形PAB的面积S=
×1×
=
.
由余弦定理得,BC2=AB2+AC2-2AB•ACcos∠BAC
=1+9-2×1×3×(-
| 1 |
| 2 |
所以BC=
| 13 |
(2)因为P为∠BAC平分线上异于A的一点,所以∠PAB=60°,
又∠APB=30°,则∠ABP=180°-60°-30°=90°,
又AB=1,则PB=
| 3 |
所以三角形PAB的面积S=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
点评:本题考查余弦定理,内角和定理的应用,属于基础题.

练习册系列答案
相关题目
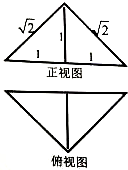
已知一个三棱锥的正视图和侧视图如图所示,则该三棱锥的俯视图可能为( )


A、 |
B、 |
C、 |
D、 |
 把边长为
把边长为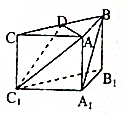 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,D为BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,D为BC的中点.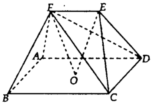 如图,O为矩形ABCD的中心,E,F为平面ABCD同侧两点,且EF
如图,O为矩形ABCD的中心,E,F为平面ABCD同侧两点,且EF