题目内容

已知A，B是平面α同侧两点，AM⊥α于M，BN⊥α于N，且AM=3，BN=5，MN=4，设P为平面α内的一个动点，则AP+BP的最小值是（　　）
A、4
5
B、5
3
C、3
5
D、8
考点：点、线、面间的距离计算,空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：作A关于α的对称点C，连接BC，与α交于P，则AP+BP的最小值是线段BC的长度，画出图形，利用两点之间线段最短解答．
解答： 解：作A关于α的对称点C，连接BC，与α交于P，则AP+BP的最小值是线段BC的长度，如图
AP+BP=CP+BP=BC，设MP=x，则NP=4-x，所以BC=
AM2+MP2
+
BN2+NP2
=
9+x2
+
25+(4-x)2
，
所以AP+BP的最小值为
80
=4
5
；
故选A．
点评：本题考查了空间线段最短问题的求法；关键是转化为两点之间的距离问题解答．
练习册系列答案
相关题目
函数 f（x）=sin（ωx+φ）+b的图象如图，则 f（x）的解析式S=f（1）+f（2）+f（3）+…+f（2015）的值分别为（　　）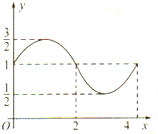
A、f（x）=
1
2
sin2πx+1，S=2015
B、f（x）=
1
2
sin2πx+1，S=2014
1
2
C、f（x）=
1
2
sin
π
2
x+1，S=2015
D、f（x）=
1
2
sin
π
2
x+1，S=2014
1
2
在△ABC中，A=30°，a=2，则
a+b+c
sinA+sinB+sinC
的值为（　　）
A、2
B、
3
C、
1
2
D、4
函数f（x）满足f（x+2）=f（x），且在x∈[0，2）时，f（x）=
2x-x2
，若直线kx-y+k=0（k＞0）与函数f（x）的图象有且仅有三个不同交点，则k的取值范围是（　　）
A、(
15
15
，
3
3
)
B、(
3
5
，
5
3
)
C、(
1
3
，
1
2
)
D、(
1
15
，
1
3
)
在△ABC中，a，b，c为其三边，若（a+c）（a-c）=b（b+c），则∠A=（　　）
A、60°或120°B、60°
C、120°D、150°
设0＜a＜1，则函数y=
1
ax-1
的图象大致为（　　）
A、
B、
C、
D、
已知向量
a
=（1，x，-3），
b
=（2，4，y），且
a
∥
b
，那么x+y等于（　　）
A、-4B、-2C、2D、4
已知公差为d的等差数列{an}满足d＞0，且a2是a1、a4的等比中项，记bn=a2n（n∈R），对任意n都有
1
b1
+
1
b2
+…+
1
bn
＜2，则公差d的取值范围是（　　）
A、[
1
2
，+∞）
B、（
1
2
，+∞）
C、[
1
4
，
1
2
）
D、[
1
4
，
1
2
]
已知集合A={y|y=x2-
3
2
x+1，x∈[
3
4
，2]}，B={x|x+m2≥1}．
（Ⅰ）求集合A；
（Ⅱ）若p：x∈A；q：x∈B且p是q的充分条件，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网