Question

函数f（x）满足f（x+2）=f（x），且在x∈[0，2）时，f（x）=

2x-x2

，若直线kx-y+k=0（k＞0）与函数f（x）的图象有且仅有三个不同交点，则k的取值范围是（　　）

• A、(

  15

  15

  ，

  3

  3

  )
• B、(

  3

  5

  ，

  5

  3

  )
• C、(

  1

  3

  ，

  1

  2

  )
• D、(

  1

  15

  ，

  1

  3

  )

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：根据函数的周期性，作出函数f（x）的图象，利用直线和圆相切的条件求出直线斜率，利用数形结合即可得到结论．

解答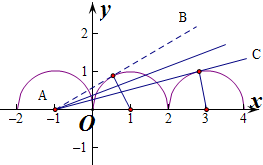： 解：由kx-y+k=0（k＞0）得y=k（x+1），（k＞0），
则直线过定点A（-1，0），
当x∈[0，2）时，f（x）=

2x-x2

，即（x-1）²+y²=1，（y≥0），
对应的根据为圆心在（1，0）的上半圆，
∵f（x）满足f（x+2）=f（x），
∴当x∈[2，4）时，（x-3）²+y²=1，（y≥0），此时圆心为（3，0），
当直线和圆（x-1）²+y²=1，（y≥0）相切时此时有2个交点，
此时圆心（1，0）到直线的距离d=

|k+k|

1+k2

=

|2k|

1+k2

=1，
解得k=

3

3

或k=-

3

3

（舍）．
当线和圆（x-3）²+y²=1，（y≥0）相切时此时有4个交点，
此时圆心（3，0）到直线的距离d=

|3k+k|

1+k2

=

|4k|

1+k2

=1，
解得k=

15

15

或k=-

15

15

（舍）．
若若直线kx-y+k=0（k＞0）与函数f（x）的图象有且仅有三个不同交点，
则直线在AB和AC之间，
则

15

15

＜k＜

3

3

，
故选：A

点评：本题主要考查函数与方程之间的应用，利用数形结合以及直线和圆心相切的等价条件是解决本题的关键．