题目内容
13.已知数列{an}中,a1=2,an+1=an+ln(1+$\frac{1}{n}$),则an=( )| A. | 2+lnn | B. | 2+(n-1)lnn | C. | lnn-2 | D. | 1+n+lnn |
分析 an+1=an+ln(1+$\frac{1}{n}$),可得an+1-an=ln$\frac{n+1}{n}$,利用“累加求和”方法与对数的运算性质即可得出.
解答 解:an+1=an+ln(1+$\frac{1}{n}$),∴an+1-an=ln$\frac{n+1}{n}$,
则an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=$ln\frac{n}{n-1}$+$ln\frac{n-1}{n-2}$+…+ln$\frac{2}{1}$+2
=ln$(\frac{n}{n-1}•\frac{n-1}{n-2}•…•\frac{3}{2}•\frac{2}{1})$+2
=lnn+2.
故选:A.
点评 本题考查了数列递推关系、累加求和方法、对数运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.某三棱锥的三视图如图所示,则俯视图的面积为( )
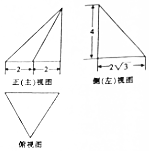

| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
4.若sin($\frac{π}{4}$-α)=$\frac{3}{5}$,-$\frac{π}{4}$<α<0,则cos2α=( )
| A. | -$\frac{24}{25}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{24}{25}$ |
1.函数$y=sin(2x+\frac{π}{3})$图象中的一条对称轴的方程是( )
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{12}$ |
8.函数f(x)=3x+$\frac{12}{x^2}$(x>0)取得最小值时x为( )
| A. | 8 | B. | 9 | C. | 2 | D. | 6$\sqrt{6}$ |
5.函数f(x)=x3-3ax2+(2a+1)x既有极小值又有极大值,则a的取值范围为( )
| A. | -$\frac{1}{3}$<a<1 | B. | a>1或a$<-\frac{1}{3}$ | C. | -1$<a<\frac{1}{3}$ | D. | a$>\frac{1}{3}$或a<-1 |