题目内容
已知正四棱锥P-ABCD的底面边长为2
,高为3,球O是正四棱锥P-ABCD的内切球,则球O的表面积为( )
| 3 |
| A、16π | ||
| B、32π | ||
| C、4π | ||
D、
|
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:运用分割思想,连接OP,OA,OB,OC,OD,得到四个三棱锥和一个四棱锥,由大的四棱锥的体积等于四个三棱锥的体积和一个小的四棱锥的体积之和,根据正四棱锥的性质,求出斜高,即可求出球的半径r,从而得到球的表面积.
解答:
解:设球的半径为r,
连接OP,OA,OB,OC,OD,得到四个三棱锥和一个四棱锥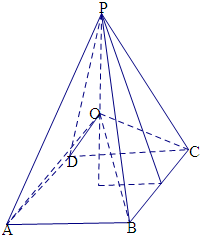
它们的高均为r,
则VP-ABCD=VO-PAB+VO-PAD+VO-PBC+VO-PCD+VO-ABCD
即
×3×(2
)2=
r(4×S△PBC+12),
由四棱锥的高和斜高,及斜高在底面的射影构成的直角三角形得到,
斜高为
=2
∴S△PBC=
×(2
)2=6,
∴r=
=1,
则球的表面积为4π.
故选C.
连接OP,OA,OB,OC,OD,得到四个三棱锥和一个四棱锥

它们的高均为r,
则VP-ABCD=VO-PAB+VO-PAD+VO-PBC+VO-PCD+VO-ABCD
即
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
由四棱锥的高和斜高,及斜高在底面的射影构成的直角三角形得到,
斜高为
32+(
|
| 3 |
∴S△PBC=
| 1 |
| 2 |
| 3 |
∴r=
| 3×12 |
| 4×6+12 |
则球的表面积为4π.
故选C.
点评:本题主要考查球与正四棱锥的关系,通过分割,运用体积转换的思想,是解决本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知a,b,c,d为偶数,且0<a<b<c<d,d-a=90,a,b,c成等差数列,b,c,d成等比数列,则a+b+c+d的值为( )
| A、384 | B、324 |
| C、284 | D、194 |
若函数f(x)=ax3+x在定义域R上恰有三个单调区间,则a的取值范围是( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、[0,+∞) |
设函数f(x)=ex(sinx-cosx)(0≤x≤2014π),则函数f(x)的各极小值之和为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
当0<x<1时,下列不等式正确的是( )
A、(
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
函数y=x3-3x的极大值为M极小值为N,则M+N=( )
| A、)4 | B、2 | C、1 | D、0 |
如果函数f(x)=
是奇函数,那么a=( )
| a•3x+2a-3 |
| 3x+1 |
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、-2 |
已知全集U={1,2,3,4,5},集合A={1,2,3},则∁UA为( )
| A、{1,3,4} |
| B、{4,5} |
| C、{0,2,4} |
| D、{0,2,3,4} |