题目内容
6.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,1),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 利用两个向量数量积的定义求得cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$ 的值,可得θ的值.
解答 解:∵向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,1),设$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为θ,
则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{\sqrt{3}+\sqrt{3}}{2•2}$=$\frac{\sqrt{3}}{2}$,∴θ=30°,
故选:A.
点评 本题主要考查两个向量数量积的定义,根据三角函数的值求角,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}(1-2a)x+3a,x<1\\ lnx,x≥1\end{array}\right.$的值域为R,那么a的取值范围是( )
| A. | $[{-1,\frac{1}{2}})$ | B. | $({-1,\frac{1}{2}})$ | C. | (-∞,-1] | D. | $({-∞,\frac{1}{2}})$ |
1.若集合M={x∈N|x2-8x+7<0},N={x|$\frac{x}{3}$∉N},则M∩N等于( )
| A. | {3,6} | B. | {4,5} | C. | {2,4,5} | D. | {2,4,5,7} |
18.若能把单位圆O:x2+y2=1的周长和面积同时分为相等的两部分的函数称为圆O的“完美函数”,下列函数不是圆O的“完美函数”的是( )
| A. | f(x)=4x3+x | B. | $f(x)=ln\frac{5-x}{5+x}$ | C. | $f(x)=tan\frac{x}{2}$ | D. | f(x)=ex+e-x |
 把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.
把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.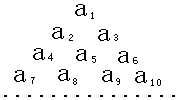 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.