表面积为3π的圆锥.它的侧面展开图是一个半圆.则该圆锥的底面半径为( )A．$\frac{{2\sqrt{15}}}{5}$B．$\frac{{\sqrt{15}}}{5}$C．2D．1 题目和参考答案——青夏教育精英家教网—

题目内容

12．表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面半径为（　　）

A．

$\frac{{2\sqrt{15}}}{5}$

B．

$\frac{{\sqrt{15}}}{5}$

C．

D．

分析设圆锥的底面的半径为r，圆锥的母线为l，则由πl=2πr得l=2r，再根据表面积S=πr²+πr•2r=3π，求得r的值，即为所求．

解答解：设圆锥的底面的半径为r，圆锥的母线为l，则由πl=2πr得l=2r，
而表面积S=πr²+πr•2r=3πr²=3π，故r²=1，解得r=1，
故选：D．

点评本题主要考查旋转体的侧面展开图，注意立体图和展开图中量的关系，属于基础题．

练习册系列答案

18．已知向量$\overrightarrow{AB}$=（2，0），$\overrightarrow{AC}$=（1，6），则（2$\overrightarrow{AB}$+3$\overrightarrow{CA}$）$•\overrightarrow{BC}$=（　　）

15．若函数f（x）在x=a处的导数为A（aA≠0），函数F（x）=f（x）-A²x²满足F′（a）=0，则A=$\frac{1}{2a}$．

7．已知a＞0，a≠1，x＞0，则“a＞2”是“log_a$\frac{x+1}{2}$≥$\frac{1}{2}$log_ax”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

17．已知向量$\vec a$，$\vec b$的夹角为60°，且$|{\vec a}|=2$，$|{\vec b}|=1$，当$|{\vec a-x\vec b}|$取得最小值时，实数x的值为（　　）

4．双曲线16x²-9y²=144的离心率为（　　）

1．已知f（x）=$\left\{\begin{array}{l}{|2x+3|，x∈（-6，-1）}\\{{x}^{2}，x∈[-1，1]}\\{x，（x∈[1，6]}\end{array}\right.$则f（$\sqrt{2}$）=$\sqrt{2}$，则f（-π）=2π-3．

2．

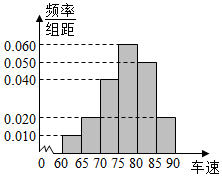2016年“双节”期间，高速公路车辆较多，某调查公司在一服务区从小型汽车中按进服务区的先后每间隔35辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段：
[60，65），[65，70），[70，75），[75，80），[80，85），[85，90）后得到如图的频率分布直方图．
（Ⅰ）求这40辆小型车辆车速的众数和中位数的估计值；
（Ⅱ）若从车速在[60，70）的车辆中任抽取2辆，求车速在[65，70）的车辆至少有一辆的概率．

试题分类