题目内容
7.已知a>0,a≠1,x>0,则“a>2”是“loga$\frac{x+1}{2}$≥$\frac{1}{2}$logax”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由a>2,可知:函数y=log2x在(0,+∞)上单调递增;可知:“loga$\frac{x+1}{2}$≥$\frac{1}{2}$logax”成立.反之不成立,因为a>1即可.
解答 解:∵a>2,可知:函数y=log2x在(0,+∞)上单调递增;
∵x>0,$\frac{x+1}{2}$≥$\sqrt{x}$,∴“loga$\frac{x+1}{2}$≥$\frac{1}{2}$logax”,当且仅当x=1时取等号.
反之不成立,因为a>1即可.
故选:A.
点评 本题考查了函数的单调性、基本不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
13.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向左平移$\frac{π}{2}$个单位,沿y轴向下平移1个单位,得到函数y=sin$\frac{1}{2}$x的图象,则y=f(x)是( )
| A. | y=sin(x+$\frac{π}{2}$)+1 | B. | y=sin(x-$\frac{π}{2}$)+1 | C. | y=sin(x+$\frac{π}{4}$)+1 | D. | y=sin(x-$\frac{π}{4}$)+1 |
12.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面半径为( )
| A. | $\frac{{2\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{5}$ | C. | 2 | D. | 1 |
19.下列说法错误的是( )
| A. | 若a,b∈R,且a+b>4,则a,b至少有一个大于2 | |
| B. | “?x0∈R,${2^{x_0}}=1$”的否定是“?x∈R,2x≠1” | |
| C. | a>1,b>1是ab>1的必要条件 | |
| D. | △ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件 |
16.关于x的不等式$\frac{x+1}{3-x}<0$的解集( )
| A. | (-∞,-1) | B. | (-∞,-1)∪(3,+∞) | C. | (-1,3) | D. | (3,+∞) |
17.已知集合M={-2,-1,0,1},N={x|1≤2x≤4,x∈Z},则M∩N=( )
| A. | {-2,-1,0,1,2} | B. | {0,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
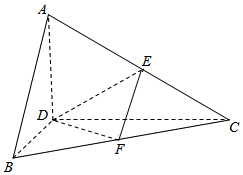 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.