题目内容
设变量x,y满足约束条件
,则目标函数z=2x+y的最小值为( )
|
| A、2 | B、3 | C、5 | D、6 |
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:由约束条件作出可行域,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答:
解:由约束条件
作出可行域如图,

化目标函数z=2x+y为y=-2x+z,
由图可知,当直线y=-2x+z过A(1,1)时直线在y轴上的截距最小,z最小,为2×1+1=3.
故选:B.
|

化目标函数z=2x+y为y=-2x+z,
由图可知,当直线y=-2x+z过A(1,1)时直线在y轴上的截距最小,z最小,为2×1+1=3.
故选:B.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、命题“若x=1则x2=1”的否命题为“若x2≠1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、“x=y”是“sinx=siny”的充分不必要条件 |
| D、“命题p,q中至少有一个为真命题”是“p或q为真命题”的充分不必要条件 |
已知
,则z=
的范围( )
|
| x+1 |
| 2y+1 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、(
|
“θ≠
”是“cosθ≠
”的( )
| π |
| 3 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn=( )
| A、2n-1 | ||
B、(
| ||
C、(
| ||
D、
|
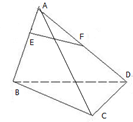 如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.
如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.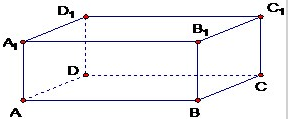 长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).
长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).