题目内容
设条件p：|x-2|＜3，条件q：0＜x＜a，其中a为正常数，若p是q的必要不充分条件，则a的取值范围是（ ）
| A、（0，5] |
| B、（0，5） |
| C、[5，+∞） |
| D、（5，+∞） |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质，以及充分条件和必要条件的定义，即可得到结论．
解答：
解：由|x-2|＜3，得-3＜x-2＜3，即-1＜x＜5，即p：-1＜x＜5，
∵q：0＜x＜a，a为正常数
∴要使若p是q的必要不充分条件，
则0＜a≤5，
故选：A．
∵q：0＜x＜a，a为正常数
∴要使若p是q的必要不充分条件，
则0＜a≤5，
故选：A．
点评：本题主要考查绝对值不等式的解法以及充分条件和必要条件的判断，比较基础．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
由一组样本数据（x1，y2），（x2，y2），…，（xn，yn）得到的回归直线方程
=bx+a，那么下面说法正确的是（ ）
| ∧ |
| y |
A、直线
| ||||||
B、直线
| ||||||
C、直线
| ||||||
D、直线
|
在直角坐标系中，终边在坐标轴上的角的集合是（ ）
A、{α|α=
| ||
B、{α|α=
| ||
C、{α|α=
| ||
| D、{α|α=kπ，k∈Z} |
集合A={x|y=
}，集合B={y|y=-
}，则有（ ）
| 1 | ||
|
| 1 | ||
|
| A、A⊆B | B、A∩B=∅ |
| C、B⊆A | D、以上均错误 |
“a≥2
”是“f（x）=x3-ax2+4x-8有极值”的（ ）
| 3 |
| A、充分而非必要条件 |
| B、充要条件 |
| C、必要而非充分条件 |
| D、既非充分又非必要条件 |
若二项式（
+x2）3展开式中的常数项为k，则直线y=kx与曲线y=x2围成的封闭图形的面积为（ ）
| 1 |
| x |
| A、3 | ||
B、
| ||
| C、9 | ||
D、
|
已知f（x）=
是（-∞，+∞）上的减函数，那么a的取值范围是（ ）
|
| A、（-∞，1] | ||||
B、[
| ||||
| C、[0，1] | ||||
D、（
|
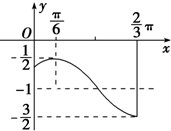如图，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜
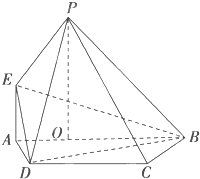如图，PO⊥平面ABCD，点O在AB上，EA∥PO，四边形ABCD为直角梯形，BC⊥AB，BC=CD=BO=PO，EA=AO=