题目内容
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中抽出500件,量其内径尺寸的结果如下表:
甲厂
乙厂
(1)由以上统计数据填下面2×2列联表,
(2)根据题(1)中表格的数据,问是否有99%的把握认为“两个分厂生产的零件的质量有差异”?说明理由.
甲厂
| 分组 | [29.86, 29.90) |
[29.90, 29.94) |
[29.94, 29.98) |
[29.98, 30.02) |
[30.02, 30.06) |
[30.06, 30.10) |
[30.10, 30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86, 29.90) |
[29.90, 29.94) |
[29.94, 29.98) |
[29.98, 30.02) |
[30.02, 30.06) |
[30.06, 30.10) |
[30.10, 30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)利用统计数据可填写2×2列联表;
(2)利用公式,求出k2,与临界值比较,即可得出结论.
(2)利用公式,求出k2,与临界值比较,即可得出结论.
解答:
解:(1)由以上统计数据填下面2×2列联表,
(2)k2=
≈7.35>6.635,
所以有99%的把握认为“两个分厂生产的零件的质量有差异”.
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | 360 | 320 | 680 |
| 非优质品 | 140 | 180 | 320 |
| 合计 | 500 | 500 | 1000 |
| 1000×(360×180-320×140)2 |
| 500×500×680×320 |
所以有99%的把握认为“两个分厂生产的零件的质量有差异”.
点评:本题重点考查独立性检验的应用,解题的关键是正确统计,运用好公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设复数z+i(z为复数)在映射f下的象为zi,则-2+2i的象是( )
| A、2-2i | B、-2-2i |
| C、1-2i | D、-1-2i |
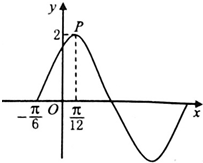 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,