题目内容
13.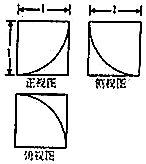 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )| A. | 6-$\frac{π}{8}$ | B. | 6-$\frac{π}{4}$ | C. | 6+$\frac{π}{8}$ | D. | 6+$\frac{π}{4}$ |
分析 根据几何体的三视图知该几何体是棱长为1是正方体,
在一个顶点处挖去半径为1的$\frac{1}{8}$球体,结合图中数据求出其表面积.
解答 解:根据几何体的三视图知,该几何体是棱长为1是正方体,
在一个顶点处挖去半径为1的$\frac{1}{8}$球体,如图所示;
则其表面积为
S=6×12-3×$\frac{1}{4}$π×12+$\frac{1}{8}$×4π×12=6-$\frac{π}{4}$.
故选:D.
点评 本题考查了几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是易错题.

练习册系列答案
相关题目
3.已知集合M={-1,0,1},N={x|(x+1)(x-1)<0},则M∩N=( )
| A. | {-1,0,1} | B. | [-1,1] | C. | {0} | D. | [0,1] |
8.已知等差数列{an}前5项和为35,a5=11,则a4=( )
| A. | 9 | B. | 10 | C. | 12 | D. | 13 |
5.“a=10“是“直线ax+4y-2=0与2x-5y+b=0互相垂直”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也必要条件 |
2.若圆心为(3,1)的圆与x轴相切,则该圆的方程是( )
| A. | x2+y2-2x-6y+9=0 | B. | x2+y2+6x+2y+9=0 | C. | x2+y2-6x-2y+9=0 | D. | x2+y2+2x+6y+9=0 |