题目内容
4.已知$tan2θ=\frac{4}{3},π<2θ<2π$(1)求tanθ的值;
(2)求$\frac{{2{{cos}^2}\frac{θ}{2}-sinθ-1}}{sin(π-θ)+cosθ}$的值.
分析 (1)根据角的范围,利用二倍角的正切公式,求得tanθ的值.
(2)利用二倍角的余弦公式、同角三角函数的基本关系,求得tanθ的值.
解答 解:(1)∵$tan2θ=\frac{2tanθ}{{1-{{tan}^2}θ}}=\frac{4}{3}$,∴$tanθ=-2或tanθ=\frac{1}{2}$,
∵π<θ<2π,∴$\frac{π}{2}$<θ<π,∴tanθ=-2.
(2)$\frac{{2{{cos}^2}\frac{θ}{2}-sinθ-1}}{sin(π-θ)+cosθ}$=$\frac{cosθ-sinθ}{sinθ+cosθ}=\frac{1-tanθ}{tanθ+1}=-3$.
点评 本题主要考查同角三角函数的基本关系的应用,二倍角公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
14.下列函数中,与函数$f(x)=\frac{1}{{\root{3}{x}}}$的定义域相同的函数是( )
| A. | y(x)=x•ex | B. | $y=\frac{sinx}{x}$ | C. | $y=\frac{x}{sinx}$ | D. | $y=\frac{lnx}{x}$ |
13.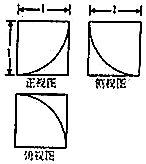 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )
 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )| A. | 6-$\frac{π}{8}$ | B. | 6-$\frac{π}{4}$ | C. | 6+$\frac{π}{8}$ | D. | 6+$\frac{π}{4}$ |
 阅读如图程序框图,并根据该程序框图回答以下问题:
阅读如图程序框图,并根据该程序框图回答以下问题: