题目内容
20.已知函数f(x)=ln x,F(x)=x-$\frac{a}{x}$+$\frac{lnx}{x}$-a,(1)求函数f(x)在A(1,0)处的切线方程.
(2)若F(x)在[1,+∞)上单调递增,求实数a的取值范围.
分析 (1)根据f′(1)=1,求出切线方程即可;
(2)求出函数F(x)的导数,问题转化为a≥-x2+ln x-1恒成立,令G(x)=-x2+ln x-1,求出G(x)的最大值,从而求出a的范围即可.
解答 解:(1)因为f′(x)=$\frac{1}{x}$,所以f′(1)=1,
故切线方程为y=x-1.__________(4分)
(2)y=F(x)在[1,+∞)上单调递增,
F′(x)=$\frac{{x}^{2}-lnx+a+1}{{x}^{2}}$,
则当x≥1时,x2-ln x+a+1≥0恒成立,
即当x≥1时,a≥-x2+ln x-1恒成立.
令G(x)=-x2+ln x-1,
则当x≥1时,G′(x)=$\frac{1-{2x}^{2}}{x}$<0,
故G(x)=-x2+ln x-1在[1,+∞)上单调递减,
从而G(x)max=G(1)=-2,
故a≥G(x)max=-2,
即a的取值范围为a≥-2._______(12分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
13.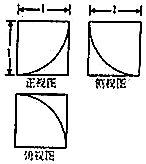 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )
 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )| A. | 6-$\frac{π}{8}$ | B. | 6-$\frac{π}{4}$ | C. | 6+$\frac{π}{8}$ | D. | 6+$\frac{π}{4}$ |
11.已知动点P(x,y)在椭圆C:$\frac{x^2}{25}+\frac{y^2}{16}$=1上,F为椭圆C的右焦点,若点M满足|$\overrightarrow{MF}$|=1且$\overrightarrow{PM}•\overrightarrow{MF}$=0,则|$\overrightarrow{PM}$|的最小值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{12}{5}$ | D. | 1 |
8.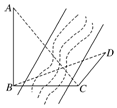 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | 10米 | B. | 2$\sqrt{6}$米 | C. | $2\sqrt{3}$米 | D. | $3\sqrt{2}$米 |
5.若方程x2+(m+2)x+m+5=0只有负根,则m的取值范围是( )
| A. | m≥4 | B. | -5<m≤-4 | C. | -5≤m≤-4 | D. | -5<m<-2 |
9.已知随机变量X服从正态分布N(μ,σ2),μ=4,σ=1,则P(5<X<6)=( )
| A. | 0.1358 | B. | 0.1359 | C. | 0.2176 | D. | 0.2718 |