题目内容
3.已知集合M={-1,0,1},N={x|(x+1)(x-1)<0},则M∩N=( )| A. | {-1,0,1} | B. | [-1,1] | C. | {0} | D. | [0,1] |
分析 求出关于集合N的范围,求出M、N的交集即可.
解答 解:集合M={-1,0,1},N={x|(x+1)(x-1)<0}={x|-1<x<1},
则M∩N={0},
故选:C.
点评 本题考查了集合的运算,考查交集的定义,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.设函数的定义域为D,若满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域为$[{\frac{a}{2},\frac{b}{2}}]$,则称f(x)为“倍缩函数”.若函数f(x)=ex+t为“倍缩函数”,则实数t的取值范围是( )
| A. | $({-∞,-\frac{1+ln2}{2}}]$ | B. | $({-∞,-\frac{1+ln2}{2}})$ | C. | $[{\frac{1+ln2}{2},+∞})$ | D. | $({\frac{1+ln2}{2},+∞})$ |
14.下列函数中,与函数$f(x)=\frac{1}{{\root{3}{x}}}$的定义域相同的函数是( )
| A. | y(x)=x•ex | B. | $y=\frac{sinx}{x}$ | C. | $y=\frac{x}{sinx}$ | D. | $y=\frac{lnx}{x}$ |
11.函数f(x)=axn(2-x)2在区间[0,2]上的图象如图所示,则n的值可能是( )


| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
13.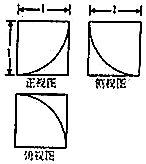 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )
 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )| A. | 6-$\frac{π}{8}$ | B. | 6-$\frac{π}{4}$ | C. | 6+$\frac{π}{8}$ | D. | 6+$\frac{π}{4}$ |