题目内容
8.已知等差数列{an}前5项和为35,a5=11,则a4=( )| A. | 9 | B. | 10 | C. | 12 | D. | 13 |
分析 设等差数列的首项为a1,由已知列式求得a1,进一步求得公差,再由通项公式求得a4 .
解答 解:设等差数列的首项为a1,
∵a5=11,S5=35,
∴${S}_{5}=\frac{({a}_{1}+{a}_{5})×5}{2}=\frac{({a}_{1}+11)×5}{2}=35$,
解得:a1=3.
∴d=$\frac{{a}_{5}-{a}_{1}}{4}=\frac{11-3}{4}=2$.
∴a4=a1+3d=3+3×2=9.
故选:A.
点评 本题考查等差数列的通项公式,考查等差数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
13.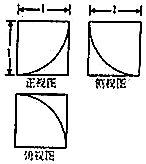 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )
 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )| A. | 6-$\frac{π}{8}$ | B. | 6-$\frac{π}{4}$ | C. | 6+$\frac{π}{8}$ | D. | 6+$\frac{π}{4}$ |
17.点P是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的一点,其左焦点为F(-c,0),若M为线段FP的中点,且M到坐标原点的距离为$\frac{c}{4}$,则$\frac{b}{a}$的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{3}$) | B. | (0,$\frac{\sqrt{5}}{3}$] | C. | ($\frac{\sqrt{5}}{3}$,1) | D. | [$\frac{\sqrt{5}}{3}$,1) |
 阅读如图程序框图,并根据该程序框图回答以下问题:
阅读如图程序框图,并根据该程序框图回答以下问题: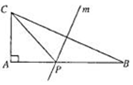 如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.
如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.