题目内容
5.“a=10“是“直线ax+4y-2=0与2x-5y+b=0互相垂直”的( )| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也必要条件 |
分析 直线ax+4y-2=0与2x-5y+b=0互相垂直,则$-\frac{a}{4}×(-\frac{2}{-5})$=-1,解得a即可判断出结论.
解答 解:直线ax+4y-2=0与2x-5y+b=0互相垂直,则$-\frac{a}{4}×(-\frac{2}{-5})$=-1,解得a=10.
∴“a=10“是“直线ax+4y-2=0与2x-5y+b=0互相垂直”的充要条件.
故选:A.
点评 本题考查了相互垂直的直线斜率之间的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
13.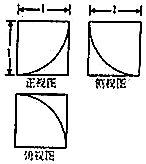 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )
 一个几何体的三视图如图所示,则其表面积为( )
一个几何体的三视图如图所示,则其表面积为( )| A. | 6-$\frac{π}{8}$ | B. | 6-$\frac{π}{4}$ | C. | 6+$\frac{π}{8}$ | D. | 6+$\frac{π}{4}$ |
17.点P是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的一点,其左焦点为F(-c,0),若M为线段FP的中点,且M到坐标原点的距离为$\frac{c}{4}$,则$\frac{b}{a}$的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{3}$) | B. | (0,$\frac{\sqrt{5}}{3}$] | C. | ($\frac{\sqrt{5}}{3}$,1) | D. | [$\frac{\sqrt{5}}{3}$,1) |
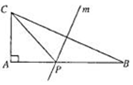 如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.
如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.