题目内容
15.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为4,过焦点且垂直于x轴的弦长为2$\sqrt{2}$.(Ⅰ)求椭圆E的方程;
(Ⅱ)过椭圆E右焦点的直线l交椭圆于点M,N,设椭圆的左焦点为F,求$\overrightarrow{FM}$•$\overrightarrow{FN}$的取值范围.
分析 (Ⅰ)由已知求出椭圆焦点坐标,并得到所过定点(2,$\sqrt{2}$),再由椭圆定义可得a,结合隐含条件求得b,则椭圆方程可求;
(Ⅱ)当直线l垂直于x轴时,求出M,N的坐标,直接求得$\overrightarrow{FM}$•$\overrightarrow{FN}$的值;当直线l不垂直于x轴,可设l的方程为y=k(x-2),联立直线方程与椭圆方程,借助于根与系数的关系及向量的坐标运算求得$\overrightarrow{FM}$•$\overrightarrow{FN}$的取值范围.
解答 解:(Ⅰ)∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距是4,∴焦点坐标是(-2,0),(2,0).
由题意可得,椭圆E过(2,$\sqrt{2}$)点,
∴2a=$\sqrt{(2-2)^{2}+(\sqrt{2}-0)^{2}}+\sqrt{(2+2)^{2}+(\sqrt{2}-0)^{2}}=4\sqrt{2}$.
则a=2$\sqrt{2}$,$b=\sqrt{{a}^{2}-{c}^{2}}=2$.
∴椭圆E的方程是$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(Ⅱ)由题意得,左焦点F(-2,0),右焦点坐标为(2,0).
若直线l垂直于x轴,则点M($2,\sqrt{2}$),N(2,-$\sqrt{2}$).
$\overrightarrow{FM}$•$\overrightarrow{FN}$=(4,$\sqrt{2}$)•(4,-$\sqrt{2}$)=14;
若直线l不垂直于x轴,可设l的方程为y=k(x-2),设点M(x1,y1),N(x2,y2).
联立$\left\{\begin{array}{l}{y=k(x-2)}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得到(1+2k2)x2-8k2x+8k2-8=0.
则${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{8{k}^{2}-8}{1+2{k}^{2}}$.
∴$\overrightarrow{FM}•\overrightarrow{FN}=({x}_{1}+2,{y}_{1})•({x}_{2}+2,{y}_{2})$=$(1+{k}^{2}){x}_{1}{x}_{2}+2(1-{k}^{2})({x}_{1}+{x}_{2})+4(1+{k}^{2})$
=$\frac{28{k}^{2}-4}{1+2{k}^{2}}=14-\frac{18}{1+2{k}^{2}}$.
∵0<$\frac{18}{1+2{k}^{2}}$<18,∴$-4<\overrightarrow{FM}•\overrightarrow{FN}<14$,
∴$\overrightarrow{FM}•\overrightarrow{FN}$的取值范围是[-4,14].
点评 本题考查椭圆的简单性质,考查直线与圆锥曲线的综合运用,属中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
| A. | (-1,0] | B. | [0,3) | C. | (3,4] | D. | (-1,3) |
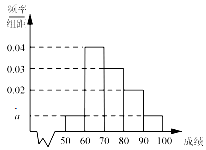 某校100名学生期中考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].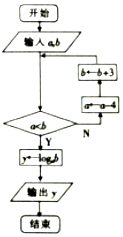 如图是一个算法的流程图,当输入a=10,b=2的时,输出的y值为3.
如图是一个算法的流程图,当输入a=10,b=2的时,输出的y值为3.