题目内容
10.已知a∈R,函数$f(x)=\frac{1}{{{2^x}-a}}$.(1)当a=0时,解不等式f(x)>1;
(2)当a>0时,求函数y=2f(x)-f(2x)的零点个数;
(3)设a<0,若对于t∈R,函数在区间[t,t+1]上的最大值与最小值之差都不超过1,求实数a的取值范围.
分析 (1)a=0时,f(x)=$\frac{1}{{2}^{x}}$,即可解不等式f(x)>1;
(2)当a>0时,换元,分类讨论,即可求函数y=2f(x)-f(2x)的零点个数;
(3)函数f(x)在区间[t,t+1]上单调递减,由题意得f(t)-f(t+1)≤1,即$\frac{1}{{2}^{t}-a}$-$\frac{1}{{2}^{t+1}-a}$≤1,设x=2t(x>0),则2x2-(3a+1)x+a2≥0,即可求实数a的取值范围.
解答 解:(1)a=0时,f(x)=$\frac{1}{{2}^{x}}$,
∵f(x)>1,即$\frac{1}{{2}^{x}}$>1,∴0<2x<1,
解得x<0.
(2)y=2f(x)-f(2x)=$\frac{2}{{2}^{x}-a}-\frac{1}{{2}^{2x}-a}$,
∴函数y=2f(x)-f(2x)的定义域为{x|x≠log2a,且x≠$\frac{1}{2}$log2a}.
令y=0得22x+1-2x-a=0,
令t=2x(t>0,且t≠a,t$≠\sqrt{a}$),方程为2t2-t-a=0,△=1+8a>0,
若a=1,t=1或-$\frac{1}{2}$,方程无解,即函数y=2f(x)-f(2x)的零点个数为0
若0<a<1或a>1,方程有两个不相等的解,即函数y=2f(x)-f(2x)的零点个数为2;
(3)函数f(x)在区间[t,t+1]上单调递减,
由题意得f(t)-f(t+1)≤1,即$\frac{1}{{2}^{t}-a}$-$\frac{1}{{2}^{t+1}-a}$≤1,
∴22t+1-(3a+1)•2t+a2≥0,
设x=2t(x>0),则2x2-(3a+1)x+a2≥0,
∴△≤0或$\left\{\begin{array}{l}{△>0}\\{\frac{3a+1}{4}≤0}\\{{a}^{2}≥0}\end{array}\right.$,∴a≤-$\frac{1}{3}$.
点评 本题主要考查函数最值的求解,以及指数不等式的应用,考查换元法、函数的零点.综合性较强,难度较大.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
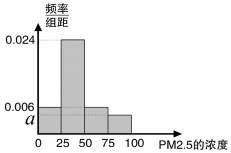 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{5}{4}$ | D. | $\frac{5}{3}$或$\frac{5}{3}$ |