题目内容
5．已知平面直角坐标系内的两个向量$\overrightarrow a=（m，3m-4）$，$\overrightarrow b=（1，2）$，且平面内的任一向量$\overrightarrow{c}$都可以唯一的表示成$\overrightarrow{c}$=$λ\overrightarrow{a}$+$μ\overrightarrow{b}$（λ，μ为实数），则m的取值范围是（ ）| A． | （-∞，4） | B． | （4，+∞） | C． | （-∞，4）∪（4，+∞） | D． | （-∞，+∞） |
分析 根据基底的定义可知：平面内的任一向量$\overrightarrow{c}$都可以唯一的表示成$\overrightarrow{c}$=$λ\overrightarrow{a}$+$μ\overrightarrow{b}$，$\overrightarrow{a}$，$\overrightarrow{b}$是平面内表示所有向量的一组基底．即$\overrightarrow{a}$，$\overrightarrow{b}$不共线即可．
解答 解：由题意可知：平面内的任一向量$\overrightarrow{c}$都可以唯一的表示成$\overrightarrow{c}$=$λ\overrightarrow{a}$+$μ\overrightarrow{b}$，
∴$\overrightarrow{a}$，$\overrightarrow{b}$是平面内表示所有向量的一组基底．
∴$\overrightarrow{a}$，$\overrightarrow{b}$必须不共线．
可得：$\frac{m}{1}≠\frac{3m-4}{2}$
解得：m≠4．
故得m的取值范围是（-∞，4）∪（4，+∞）．
故选C．
点评 本题主要考查了基底的定义的运用．基底向量肯定是非零向量，且基底并不唯一，只要不共线就行．属于基础知识考查了．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
16．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的渐近线与抛物线$y=\frac{1}{2}{x^2}+2$相切，则该双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | $\sqrt{6}$ |
10．设l，m表示不同直线，α，β表示不同平面，则下列结论中正确的是（ ）
| A． | 若l∥α，l⊥m，则m⊥α | B． | 若l∥α，l⊥m，m?β，则α⊥β | ||
| C． | 若l∥α，l∥m，则m∥α | D． | 若α∥β，l∥α，l∥m，m?β，则m∥β |
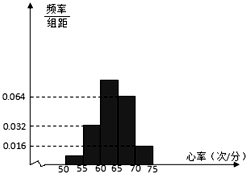某高校要了解在校学生的身体健康状况，随机抽取了50名学生进行心率测试，心率全部介于50次/分到75次/分之间，现将数据分成五组，第一组[50，55），第二组[55，60）…第五组[70，75]，按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三组的频率之比为a：4：10．