题目内容
5.已知向量$\overrightarrow{O{P}_{1}}$,$\overrightarrow{O{P}_{2}}$,$\overrightarrow{O{P}_{3}}$,满足$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=0,且|$\overrightarrow{O{P}_{1}}$|=|$\overrightarrow{O{P}_{2}}$|=|$\overrightarrow{O{P}_{3}}$|=1,则|$\overrightarrow{{P}_{1}{P}_{2}}$|=$\sqrt{3}$.分析 先证明$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$=-$\frac{1}{2}$,由向量的数量积的定义可得,∠P1OP2=120°,即可得出结论.
解答 解:∵$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=$\overrightarrow{0}$,
∴$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$=-$\overrightarrow{O{P}_{3}}$,
∵|$\overrightarrow{O{P}_{1}}$|=|$\overrightarrow{O{P}_{2}}$|=|$\overrightarrow{O{P}_{3}}$|=1,
∴两边平方,整理可得$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$=-$\frac{1}{2}$
由向量的数量积的定义可得,∠P1OP2=120°
∴|$\overrightarrow{{P}_{1}{P}_{2}}$|=$\sqrt{1+1-2×1×1×(-\frac{1}{2})}$=$\sqrt{3}$
故答案为$\sqrt{3}$.
点评 本题考查向量的数量积的定义,考查余弦定理,属于中档题.

练习册系列答案
相关题目
2.几何体的三视图如图所示,该几何体的体积为( )
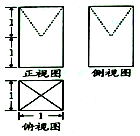

| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{3}$ |
3.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女,若从这6名教师中任选2名,选出的2名教师来自同一学校的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
13.设f(x)=cos$\frac{1}{x}$,则f′($\frac{2}{π}$)=( )
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{{π}^{2}}{4}$ |
20.执行如图所示的程序框图,若输入n的值为8,则输出S的值为( )


| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
10.已知x,y都是实数,命题p:|x|<1;命题q:x2-2x-3<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
17.设等差数列{an}的前n项和为Sn,已知a1+a2+a3=a4+a5,S5=60,则a10=( )
| A. | 16 | B. | 20 | C. | 24 | D. | 26 |