题目内容
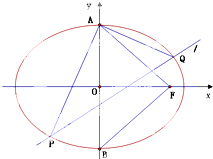 如图所示,A、B分别是椭圆C:
如图所示,A、B分别是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(1)求椭圆的方程;
(2)若不过点A的直线l与椭圆相交于P、Q两点,且AP⊥AQ,求证:直线l过定点.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出抛物线的焦点,由S△ABC=
,得到bc=
,运用a,b,c的关系,求出a,b,即可得到椭圆的方程;
(2)设直线l:y=kx+t,联立椭圆方程,消去y,得到关于x的方程,运用韦达定理和斜率公式,化简即可得到
t=1或-
,从而说明直线l经过定点.
| 2 |
| 2 |
(2)设直线l:y=kx+t,联立椭圆方程,消去y,得到关于x的方程,运用韦达定理和斜率公式,化简即可得到
t=1或-
| 1 |
| 2 |
解答:
(1)解:∵抛物线y2=4
x的焦点为(
,0),
∴椭圆C焦点F为(
,0),
即c=
,a2-b2=2,又S△ABC=
,
即bc=
则b=1,a2=3,
∴椭圆方程为
+y2=1;
(2)证明:设直线l:y=kx+t,p(x1,y1),Q(x2,y2),
又
+y2=1,联立直线方程与椭圆方程,消去y,即有
x2+3(k2x2+2ktx+t2)-3=0,(1+3k2)x2+bktx+(3t2-3)=0
x1+x2=
,x1x2=
,
又∵AP⊥AQ,
∴kAP•kAQ=-1即
•
=-1,
即y1y2-(y1+y2)+1+x1x2=0,(kx1+t)(kx2+t)-[k(x1+x2)+2t]+1+x1x2=0,
∴(1+k2)x1x2+(kt-k)(x1+x2)+t2-2t+1=0,
即(1+k2)•
+k(t-1)•
+t2-2t+1=0,
即
+(t-1)2=0
即(t-1)(4t+2)=0,
∴t=1或-
,
故直线l恒过定点(0,1),(0,-
).
| 2 |
| 2 |
∴椭圆C焦点F为(
| 2 |
即c=
| 2 |
| 2 |
即bc=
| 2 |
∴椭圆方程为
| x2 |
| 3 |
(2)证明:设直线l:y=kx+t,p(x1,y1),Q(x2,y2),
又
| x2 |
| 3 |
x2+3(k2x2+2ktx+t2)-3=0,(1+3k2)x2+bktx+(3t2-3)=0
x1+x2=
| -6kt |
| 1+3k2 |
| 3t2-3 |
| 1+3k2 |
又∵AP⊥AQ,
∴kAP•kAQ=-1即
| y1-1 |
| x1 |
| y2-1 |
| x2 |
即y1y2-(y1+y2)+1+x1x2=0,(kx1+t)(kx2+t)-[k(x1+x2)+2t]+1+x1x2=0,
∴(1+k2)x1x2+(kt-k)(x1+x2)+t2-2t+1=0,
即(1+k2)•
| 3t2-3 |
| 1+3k2 |
| -6kt |
| 1+3k2 |
即
| 3[(t2-1)-k2(t-1)2] |
| 1+3k2 |
即(t-1)(4t+2)=0,
∴t=1或-
| 1 |
| 2 |
故直线l恒过定点(0,1),(0,-
| 1 |
| 2 |
点评:本题主要考查椭圆的方程和性质,考查直线与椭圆联立,运用韦达定理,解决问题是解析几何中常用的方法,必须掌握.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
抛物线y=3x2的焦点坐标是( )
A、(0,
| ||
B、(0,-
| ||
C、(0,-
| ||
D、(0,
|
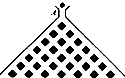 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是