题目内容
已知椭圆C：
+
=1（a＞b＞0）的离心率为
，右焦点F2到直线
+
=0的距离为1．
（1）求椭圆的C方程；
（2）已知直线y=k（x-2）（k≠0）与椭圆C相交于M、N两点，在轴x上是否存在定点E，使
•
为定值？若存在，求出E点的坐标和定值；若不存在，说明理由．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| x |
| a |
| y |
| b |
（1）求椭圆的C方程；
（2）已知直线y=k（x-2）（k≠0）与椭圆C相交于M、N两点，在轴x上是否存在定点E，使
| EM |
| EM |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由题意得e=
=
，
=1，由此能求出椭圆的方程．
（2）由
，得（1+3k2）x2-12k2x+12k2-6=0．设M（x1，y1），N（x2，y2），由此利用韦达定理结合已知条件能求出
•
=m2-6=-
为定值时，定点为E（
，0）．
| c |
| a |
| ||
| 3 |
| |bc| | ||
|
（2）由
|
| EM |
| EN |
| 5 |
| 9 |
| 7 |
| 3 |
解答：
解：（1）由e=
=
，得c=
a，①
又在右焦点F2（c，0）到直线
+
=0的距离为d=1，
得
=1，②
由①②，得a2=6，b2=2，
∴椭圆的方程为
+
=1．
（2）由
，得（1+3k2）x2-12k2x+12k2-6=0．
设M（x1，y1），N（x2，y2），∴x1+x2=
，x1x2=
，
根据题意，假设x轴上存在定点E（m，0），使得
•
为定值，
则有
•
=(x1-m，y1)•（x2-m，y2）=（x1-m）（x2-m）+y1y2
=（x1-m）（x2-m）+k2（x1-2）（x2-2）
=(k2+1)x1x2-(2k2+m)(x1+x2)+（4k2+m2）
=（k2+1）•
-（2k2+m）•
+(4k2+m2)
=
，
更使上式为定值，即与k无关，则应使3m2-12m+10=3（m2-6），
解得m=
，此时
•
=m2-6=-
为定值，定点为E（
，0）．
| c |
| a |
| ||
| 3 |
| ||
| 3 |
又在右焦点F2（c，0）到直线
| x |
| a |
| y |
| b |
得
| |bc| | ||
|
由①②，得a2=6，b2=2，
∴椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
（2）由
|
设M（x1，y1），N（x2，y2），∴x1+x2=
| 12k2 |
| 1+3k2 |
| 12k2-6 |
| 1+3k2 |
根据题意，假设x轴上存在定点E（m，0），使得
| EM |
| EN |
则有
| EM |
| EN |
=（x1-m）（x2-m）+k2（x1-2）（x2-2）
=(k2+1)x1x2-(2k2+m)(x1+x2)+（4k2+m2）
=（k2+1）•
| 12k2-6 |
| 1+3k2 |
| 12k2 |
| 1+3k2 |
=
| (3m2-12m+10)k2+(m2-6) |
| 3k2+1 |
更使上式为定值，即与k无关，则应使3m2-12m+10=3（m2-6），
解得m=
| 7 |
| 3 |
| EM |
| EN |
| 5 |
| 9 |
| 7 |
| 3 |
点评：本题考查椭圆方程的求法，考查使向量的数量积为定值的x轴上的定点是否存在的判断与求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
优学名师名题系列答案
相关题目
在△ABC中，角A，B，C所对的边分别为a，b，c，若A=30°且b=
a，则角C等于（ ）
| 3 |
| A、30° | B、60° |
| C、90° | D、30°或90° |
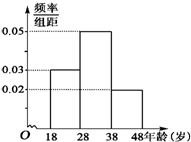武汉电视台为了宣传武汉城市圈的情况，特举办了一期有奖知识问答活动，活动对18～48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”，统计数据结果如表：
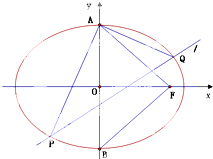如图所示，A、B分别是椭圆C：
在长方体ABCD-A1B1C1D1中，AD=AA1=3，AB=
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程）．被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．