题目内容
求函数f(x)=x2lnx的单调区间和极值.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:首先考虑函数的定义域优先原则求出定义域,然后对函数求导,导函数小于等于零,函数是单调减函数,求出减区间,即可得到单调增区间,也可获得极值.
解答:
解:由题意可知函数的定义域为:(0,+∞)
又f′(x)=2x•lnx+x2•
=2x•lnx+x,
由f′(x)≤0知,2x•lnx+x≤0,
∴0≤x≤e-
,
又因为x>0,所以函数的递减区间是(0,e-
].函数的单调增区间为(e-
,+∞),
函数在x=e-
时函数取得极小值:y极小=f(e-
)=-
.
又f′(x)=2x•lnx+x2•
| 1 |
| x |
由f′(x)≤0知,2x•lnx+x≤0,
∴0≤x≤e-
| 1 |
| 2 |
又因为x>0,所以函数的递减区间是(0,e-
| 1 |
| 2 |
| 1 |
| 2 |
函数在x=e-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2e |
点评:此题考查的是函数的单调性和导数知识的综合问题.在解答过程当中充分体现了定义于优先的原则、求导的思想、问题转化的思想.值得同学们体会反思.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
A,B,C是球O的一个截面的内接三角形的三个顶点,其中AB=
,∠C=30°,球心O到该截面的距离等于球半径的一半,则球O的表面积是( )
| 3 |
| A、18π | B、16π |
| C、14π | D、12π |
要得到函数y=2sin2x的图象,只需将函数y=2sin(2x-
)的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 如图,直三棱柱ABC-A1B1C1底面边长均为
如图,直三棱柱ABC-A1B1C1底面边长均为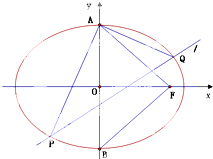 如图所示,A、B分别是椭圆C:
如图所示,A、B分别是椭圆C: