题目内容
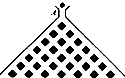 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是| 1 |
| 2 |
m-1 n-1 |
| 1 |
| 2 |
(Ⅰ)求P(4,1),P(4,2)的值;
(Ⅱ)已知f(x)=
|
考点:离散型随机变量的期望与方差,二项式定理的应用
专题:概率与统计
分析:(Ⅰ)由题意利用n次独立重复试验中事件A恰好有k次发生的概率计算公式能求出P(4,1)和P(4,2).
(Ⅱ)由题意知ξ=3,2,1,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
(Ⅱ)由题意知ξ=3,2,1,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
解答:
解:(Ⅰ)由题意知P(4,1)=
(
)3=
.
P(4,2)=
(
)(
)2=
.
(Ⅱ)由题意知ξ=3,2,1,
P(ξ=3)=P(6,1)+P(6,6)=
,
P(ξ=2)=P(6,2)+P(6,5)=
,
P(ξ=1)=P(6,3)+P(6,4)=
,
∴ξ的分布列为:
∴Eξ=3×
+2×
+1×
=
.
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 4 |
P(4,2)=
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
(Ⅱ)由题意知ξ=3,2,1,
P(ξ=3)=P(6,1)+P(6,6)=
| 1 |
| 16 |
P(ξ=2)=P(6,2)+P(6,5)=
| 5 |
| 16 |
P(ξ=1)=P(6,3)+P(6,4)=
| 5 |
| 8 |
∴ξ的分布列为:
| ξ | 3 | 2 | 1 | ||||||
| P |
|
|
|
| 1 |
| 16 |
| 5 |
| 6 |
| 5 |
| 8 |
| 23 |
| 16 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1底面边长均为
如图,直三棱柱ABC-A1B1C1底面边长均为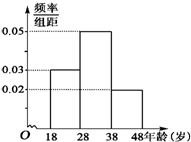 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表: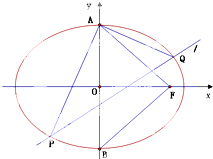 如图所示,A、B分别是椭圆C:
如图所示,A、B分别是椭圆C: