题目内容
在极坐标系中,直线l与曲线C的极坐标方程分别是ρcos(θ+
)=
和ρsin2θ=4cosθ,直线l与曲线C交于两点A,B,求线段AB的长.
| π |
| 4 |
3
| ||
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,联立方程组求得交点的坐标,可得弦长.
解答:
解:把直线l与的极坐标方程ρcos(θ+
)=
化为直角坐标方程为
x-
y=
,即x-y-3=0.
曲线C:ρsin2θ=4cosθ的直角坐标方程为y2=4x,
解方程组
,求得
,或
,可得A(1,-2)、B(9,6),
∴弦长AB=
=8
.
| π |
| 4 |
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
曲线C:ρsin2θ=4cosθ的直角坐标方程为y2=4x,
解方程组
|
|
|
∴弦长AB=
| (9-1)2+(6+2)2 |
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,求两条曲线的交点坐标,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
圆O的弦AB,CD相交于点P,已知P是AB的中点,AB=12,PC=4,那么PD=( )
| A、16 | B、9 | C、8 | D、4 |
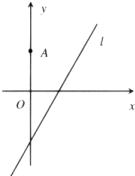 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.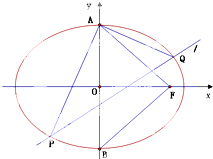 如图所示,A、B分别是椭圆C:
如图所示,A、B分别是椭圆C: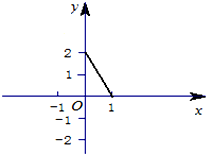 已知函数y=f(x)是定义在[-1,1]上的奇函数,当x∈(0,1]时的图象如图所示.
已知函数y=f(x)是定义在[-1,1]上的奇函数,当x∈(0,1]时的图象如图所示.